Univerzální vlastnost
Univerzální vlastnost je v matematice v teorii kategorií vlastnost, která charakterizuje výsledek určitých konstrukcí (až na izomorfismus). Univerzální vlastnost lze díky tomu použít pro definici určitých objektů nezávisle na metodě použité pro jejich konstrukci. Například definice celých čísel z přirozených čísel, racionálních čísel z celých čísel, reálných čísel z racionální čísel a okruhů polynomů z těles jejich koeficientů mohou být všechny provedeny z hlediska univerzálních vlastností. Konkrétně koncept univerzální vlastnosti umožňuje jednoduchý důkaz, že všechny konstrukce reálných čísel jsou ekvivalentní: stačí dokázat, že vyhovují stejné univerzální vlastnosti.
Technicky je univerzální vlastnost definována v pojmech kategorií a funktorů pomocí univerzálního morfismu (viz Formální definice níže). Univerzální morfismy bychom také mohli uvažovat abstraktněji jako iniciální nebo terminální objekty čárkové kategorie (viz Souvislost s čárkovými kategoriemi níže).
Univerzální vlastnosti se v matematice objevují skoro všude a použití tohoto konceptu umožňuje použití obecných vlastností univerzálních vlastností pro snadné důkazy některých vlastností, které by se jinak dokazovaly obtížně nebo zdlouhavě. Je-li například dán komutativní okruh R, podílové těleso faktorokruhu okruhu R podle prvoideálu p lze identifikovat s tělesem zbytkových tříd lokalizace okruhu R v p; což je (všechny tyto konstrukce lze definovat pomocí univerzálních vlastností).
K dalším objektům, které lze definovat univerzálními vlastnostmi, patří: všechny volné objekty, přímé produkty a přímé součty, volné grupy, volné svazy, Grothendieckovy grupy, zúplnění metrického prostoru, zúplnění okruhu, Dedekindovo–MacNeillovo zúplnění, součinové topologie, Stoneova–Čechova kompaktifikace, tenzorové součiny, inverzní limity a přímé limity, jádra a cokernely, faktorové grupy, kvocientní vektorové prostory a jiné kvocientní prostory.
Motivace
[editovat | editovat zdroj]Před uvedením formální definice univerzální vlastnosti uvedeme některé motivace pro studium takových konstrukcí.
- Konkrétní detaily dané konstrukce mohou být komplikované, ale, pokud konstrukce splňuje univerzální vlastnost, můžeme zapomenout na všechny tyto detaily: je třeba znát o konstrukce je už obsahoval v univerzální vlastnost. Důkazy často se stane krátký a elegantní, pokud univerzální vlastnost se používá místo konkrétní detaily. Například tenzorovou algebru vektorového prostoru je nepatrně složitější zkonstruovat, ale je mnohem snazší s nimi pracovat díky jeho univerzální vlastnosti.
- Univerzální vlastnosti definuje objekty jednoznačně až na jediný izomorfismus.[1] Proto jednou strategií, jak dokázat, že dva objekty jsou izomorfní, je ukázat, že vyhovují stejné univerzální vlastnosti.
- Univerzální konstrukce jsou svou povahou funktoriální: pokud můžeme provést konstrukci pro každý objekt v kategorii C, pak dostáváme funktor na C. Tento funktor je navíc pravým nebo levým adjunktem funktoru U použitého v definici univerzální vlastnosti.[2]
- Univerzální vlastnosti se objevují všude v matematice. Porozuměním jejich abstraktním vlastnostem dostáváme informace o všech těchto konstrukcích a můžeme se vyhnout opakování stejné analýzy pro každou jednotlivou instanci.
Formální definice
[editovat | editovat zdroj]Pro pochopení definice univerzální konstrukce, je důležité se podívat na příklady. Univerzální konstrukce byly ne definovaný z tenké vzduch, ale byly spíše definovaný, když si matematici začali všímat určitého vzoru v mnoha matematických konstrukcích (viz Příklady níže). Definice nám tedy nemusí dávat smysl napoprvé, ale stane se jasnou, když se uvede v soulad s konkrétními příklady.
Nechť je funktor mezi kategoriemi a . Dále nechť je objekt z , a jsou objekty z , a je morfismus v .
Pak funktor převádí , a v na , a v .
Univerzální morfismus z do je jedinečná dvojice v která má následující vlastnost, obvykle označovanou jako univerzální vlastnost:
Pro libovolný morfismus tvaru v , existuje jediný morfismus v takový, že následující diagram komutuje:

Tento kategoriální koncept můžeme dualizovat. Univerzální morfismus z do je jediná dvojice která vyhovuje následující univerzální vlastnosti:
Pro libovolný morfismus tvaru v existuje jediný morfismus v takový, že následující diagram komutuje:

Všimněte si, že v druhém diagramu jsou šipky obrácené. Obě definice jsou nezbytné pro popis univerzálních konstrukcí, které se vyskytují v matematice; ale také se objevují kvůli inherentní dualitě přítomné v teorii kategorií. V obou případech říkáme, že dvojice která se chová, jak je uvedeno výše, splňuje univerzální vlastnost.
Příklady
[editovat | editovat zdroj]Produkty
[editovat | editovat zdroj]Kategoriální součin lze charakterizovat univerzální konstrukcí. Konkrétně můžeme uvažovat kartézský součin v Set, přímý součin v Grp nebo součinovou topologii v Top, kde existují produkty.
Nechť a jsou objekty kategorie s konečnými produkty. Součin a je objekt × spolu s dvěma morfismy
- :
- :
takovými, že pro libovolný jiný objekt z a morfismy a existuje jediný morfismus takový, že a .
Pro pochopení této charakterizace jako univerzální vlastnosti uvažujme kategorii jako produktovou kategorii a definujme diagonální funktor
vztahy a . Pak je univerzální morfismus z do objektu z : pokud je libovolný morfismus ze do , pak musí být roven morfismu z do následovanému . Vyjádřeno komutativním diagramem:
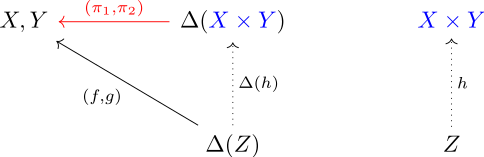
V případě kartézského součinu v Set je morfismus tvořen dvěma projekcemi a . Je-li dána libovolná množina a unikátní zobrazení takové, že požadovaný diagram komutuje, popisuje vztah .[3]
Historie
[editovat | editovat zdroj]Univerzální vlastnosti různých topologických konstrukcí prezentoval Pierre Samuel v roce 1948. Později je široce používal Nicolas Bourbaki. Blízce příbuzný koncept adjungovaných funktorů představil nezávisle Daniel Kan v roce 1958.
Odkazy
[editovat | editovat zdroj]Poznámky
[editovat | editovat zdroj]- ↑ Jacobson 2009, Proposition 1.6, p. 44.
- ↑ Milies a Sehgal 2002, p. 133, exercise 1, about the universal property group rings.
- ↑ Fong a Spivak.
Reference
[editovat | editovat zdroj]V tomto článku byl použit překlad textu z článku Universal property na anglické Wikipedii.
- COHN, Paul, 1981. Universal Algebra. Holland: D.Reidel Publishing. ISBN 90-277-1213-1..
- MAC LANE, Saunders, 1998. Categories for the Working Mathematician. 2. vyd. [s.l.]: Springer. (Graduate Texts in Mathematics 5). ISBN 0-387-98403-8.
- BORCEUX, F., 1994. Handbook of Categorical Algebra: vol 1 Basic category theory. [s.l.]: Cambridge University Press. (Encyclopedia of Mathematics and its Applications). Dostupné online. ISBN 0-521-44178-1.
- BOURBAKI, Nicolas, 1970. Livre II : Algèbre. [s.l.]: Hermann. ISBN 0-201-00639-1..
- MILIES, César Polcino; SEHGAL, Sudarshan K., 2002. An introduction to group rings. [s.l.]: Springer. (Algebras and applications, Volume 1). ISBN 978-1-4020-0238-0.
- JACOBSON, 2009. Basic Algebra II. [s.l.]: Dover. ISBN 0-486-47187-X.
- FONG, Brendan; SPIVAK, David I. Seven Sketches in Compositionality: An Invitation to Applied Category Theory. [s.l.]: [s.n.], 2018-10-12.
Související články
[editovat | editovat zdroj]- Volný objekt
- Přirozená transformace
- Adjungovaný funktor
- Monáda (teorie kategorií)
- Varieta algeber
- Kartézsky uzavřená kategorie
Externí odkazy
[editovat | editovat zdroj]- nLab, wiki projekt o matematice, fyzice a filozofii s důrazem na n-kategoriální pohled
- André Joyal, CatLab, Wiki projekt pro prezentaci teorie kategorií
- HILLMAN, Chris, 2001. A Categorical Primer [online]. 2001. Formální úvod do teorie kategorií. Dostupné v archivu pořízeném z originálu dne 1997-05-03.
- ADÁMEK, Jiří; HERRLICH, Horst; STRECKER, George E., 2004. Abstract and Concrete Categories; The Joy of Cats [online]. 2004 [cit. 2020-09-19]. Dostupné v archivu pořízeném z originálu dne 2015-04-21.
- Stanford Encyclopedia of Philosophy: “Category Theory“ – autor Jean-Pierre Marquis. Rozsáhlá bibliografie.
- Seznam konferencí o teorii kategorií
- Baez, John, 1996,“The Tale of n-categories.“ Neformální úvod do kategorií vyššího řádu.
- WildCats – balíček pro systém Mathematica věnovaný teorii kategorií. Manipulace a vizualizace objektů, morfismy, kategorie, funktory, přirozené transformace, univerzální vlastnosti.
- The catsters, YouTube kanál o teorii kategorií.
- Video archive záznamy přednášek o kategoriích, logice a základech fyziky.
- Interaktivní stránka, která generuje příklady kategorických konstrukcí v kategorii konečných množin.


















































