Kanovo rozšíření

Kanova rozšíření jsou univerzální konstrukce v matematickém oboru teorie kategorií. Jsou úzce spjaty s adjunkty, ale také s limitami a endomorfismy. Jsou pojmenovány po Danielu M. Kanovi, který v roce 1960 zkonstruoval určitá (Kanova) rozšíření pomocí limit.

Kanovo rozšíření bylo ještě před svým pojmenováním, v roce 1956, použito v homologické algebře pro výpočet odvozených funktorů.

Saunders Mac Lane ve své knize Categories for the Working Mathematician pojmenoval jednu část „Všechny koncepty jsou Kanova rozšíření“, a dále napsal, že

Pojem Kanových rozšíření zahrnuje všechny ostatní základní koncepty teorie kategorií.

Kanova rozšíření zobecňují koncept rozšíření funkce definované na podmnožině na funkci definovanou na celé množině. Není překvapivé, že definice je na vysoké úrovni abstrakce. Při specialiizaci na uspořádané množiny se z ní stává známější typ otázky na omezenou optimalizaci.

Definice

Kanovo rozšíření vychází ze tří kategorií

$\mathbf {A} ,\mathbf {B} ,\mathbf {C}$

a dvou funktorů

$X:\mathbf {A} \to \mathbf {C} ,F:\mathbf {A} \to \mathbf {B}$,

a existuje ve dvou variantách: „levé“ Kanovo rozšíření a „pravé“ Kanovo rozšíření funktoru $X$ podle $F$.

Abstraktně lze říci, že funktor $F$ dává pullback zobrazení $F^{*}:\langle B,C\rangle \to \langle A,C\rangle$. Levé a pravé adjunkty na $F^{*}$ (pokud existují) aplikované na $X$ dávají levé a pravé Kanovo rozšíření. Vyjádřením definice adjunktů, dostaneme následující definice;

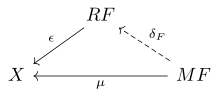
Pravé Kanovo rozšíření odpovídá nalezení čárkované šipky a přirozené transformace $\varepsilon$ v následujícím diagramu:

Formálně pravé Kanovo rozšíření $X$ podle $F$ sestává z funktoru $R:\mathbf {B} \to \mathbf {C}$ a přirozené transformace $\varepsilon :RF\to X$, která je kouniverzální podle specifikace, v tom smyslu, že pro libovolný funktor $M:\mathbf {B} \to \mathbf {C}$ a přirozenou transformaci $\mu :MF\to X$, je definována jediná přirozená transformace $\delta :M\to R$ a vyhovuje komutativnímu diagramu:

kde $\delta _{F}$ je přirozená transformace s $\delta _{F}(a)=\delta (Fa):MF(a)\to RF(a)$ pro libovolný objekt $a$ z $\mathbf {A} .$

Funktor R se často píše $\operatorname {Ran} _{F}X$.

Stejně jako u ostatních univerzálních konstruktů v teorii kategorií je „levá“ verze Kanova rozšíření duální k „pravé“ verzi, kterou získáme nahrazením všech kategorií jejich protiklady.

Výsledkem obrácení výše uvedeného popisu je obrácení přirozených transformací.

(Připomeňme, že přirozená transformace $\tau$ mezi funktory $F,G:\mathbf {C} \to \mathbf {D}$ spočívá v tom, že má šipku $\tau (a):F(a)\to G(a)$ pro každý objekt $a$ z $\mathbf {C}$, splňující vlastnost „naturality“. Když přejdeme k opačným kategoriím, zdroj a cíl $\tau (a)$ jsou prohozeny, což způsobí, že $\tau$ působí opačným směrem).

To vede k alternativnímu popisu: levé Kanovo rozšíření $X$ podle $F$ sestává z funktoru $L:\mathbf {B} \to \mathbf {C}$ a přirozené transformace $\eta :X\to LF$, které jsou univerzální vzhledem k této specifikaci v tom smyslu, že pro jiný funktor $M:\mathbf {B} \to \mathbf {C}$ a přirozenou transformaci $\alpha :X\to MF$, existuje jediná přirozená transformace $\sigma :L\to M$ a vyhovuje komutativnímu diagramu:

kde $\sigma _{F}$ je přirozená transformace s $\sigma _{F}(a)=\sigma (Fa):LF(a)\to MF(a)$ pro libovolný objekt $a$ z $\mathbf {A}$.

Funktor L se často píše $\operatorname {Lan} _{F}X$.

Stejně jako u všech univerzálních konstrukcí platí, že pokud definovaný objekt existuje, pak je jedinečný až na jediný izomorfismus. V tomto případě to znamená, že (pro levé Kanovo rozšíření) pokud $L,M$ jsou dvě levá Kanova rozšíření $X$ podle $F$ a $\eta ,\alpha$ jsou odpovídající transformace, pak existuje jediný izomorfismus funktorů $\sigma :L\to M$ takový, že druhý diagram výše komutuje. Obdoba platí pro pravé Kanovo rozšíření.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Kan extension na anglické Wikipedii.

• CARTAN, Henri; EILENBERG, Samuel, 1956. Homological algebra. Princeton, New Jersey: Princeton University Press. (Princeton Mathematical Series). 
• MAC LANE, Saunders, 1998. Categories for the Working Mathematician. 2. vyd. New York, NY: Springer-Verlag. (Graduate Texts in Mathematics). ISBN 0-387-98403-8. 

Externí odkazy

• Model independent proof of colimit formula for left Kan extensions
• Kan extension as a limit: an example