Rozklad čtvercové matice řádu 14 na bloky dané rozkladem
14
=
2
+
4
+
8
{\displaystyle 14=2+4+8}
V matematice bloková matice označuje matici , která je interpretována jako matice rozdělená do několika částí nazývaných bloky . Blokovou matici lze intuitivně reprezentovat jako původní matici s přidanými vodorovnými a svislými rozdělujícími linkami, které dělí původní matici na podmatice .
Nechť je
M
{\displaystyle {\boldsymbol {M}}}
m
×
n
{\displaystyle m\times n}
m
=
m
1
+
m
2
+
⋯
+
m
q
{\displaystyle m=m_{1}+m_{2}+\cdots +m_{q}}
q
{\displaystyle q}
n
=
n
1
+
n
2
+
⋯
+
n
r
{\displaystyle n=n_{1}+n_{2}+\cdots +n_{r}}
r
{\displaystyle r}
M
{\displaystyle {\boldsymbol {M}}}
q
r
{\displaystyle qr}
M
=
(
M
11
M
12
⋯
M
1
r
M
21
M
22
⋯
M
2
r
⋮
⋮
⋱
⋮
M
q
1
M
q
2
⋯
M
q
r
)
{\displaystyle {\boldsymbol {M}}={\begin{pmatrix}{\boldsymbol {M}}_{11}&{\boldsymbol {M}}_{12}&\cdots &{\boldsymbol {M}}_{1r}\\{\boldsymbol {M}}_{21}&{\boldsymbol {M}}_{22}&\cdots &{\boldsymbol {M}}_{2r}\\\vdots &\vdots &\ddots &\vdots \\{\boldsymbol {M}}_{q1}&{\boldsymbol {M}}_{q2}&\cdots &{\boldsymbol {M}}_{qr}\end{pmatrix}}}
kde blokové podmatice
M
i
j
{\displaystyle {\boldsymbol {M}}_{ij}}
m
i
×
n
j
{\displaystyle m_{i}\times n_{j}}
m
×
n
{\displaystyle m\times n}
m
{\displaystyle m}
n
{\displaystyle n}
m
n
{\displaystyle mn}
1
×
1
{\displaystyle 1\times 1}
Matici
M
=
(
1
1
2
2
1
1
2
2
3
3
4
4
3
3
4
4
)
{\displaystyle {\boldsymbol {M}}={\begin{pmatrix}1&1&2&2\\1&1&2&2\\3&3&4&4\\3&3&4&4\end{pmatrix}}}
lze zapsat jako blokovou matici
M
=
(
M
11
M
12
M
21
M
22
)
{\displaystyle {\boldsymbol {M}}={\begin{pmatrix}{\boldsymbol {M}}_{11}&{\boldsymbol {M}}_{12}\\{\boldsymbol {M}}_{21}&{\boldsymbol {M}}_{22}\end{pmatrix}}}
se čtyřmi bloky
2
×
2
{\displaystyle 2\times 2}
M
11
=
(
1
1
1
1
)
,
M
12
=
(
2
2
2
2
)
,
M
21
=
(
3
3
3
3
)
,
M
22
=
(
4
4
4
4
)
.
{\displaystyle {\boldsymbol {M}}_{11}={\begin{pmatrix}1&1\\1&1\end{pmatrix}},{\boldsymbol {M}}_{12}={\begin{pmatrix}2&2\\2&2\end{pmatrix}},{\boldsymbol {M}}_{21}={\begin{pmatrix}3&3\\3&3\end{pmatrix}},{\boldsymbol {M}}_{22}={\begin{pmatrix}4&4\\4&4\end{pmatrix}}.}
Přímý součet jakékoli dvojice matic
A
{\displaystyle {\boldsymbol {A}}}
m
×
n
{\displaystyle m\times n}
B
{\displaystyle {\boldsymbol {B}}}
p
×
q
{\displaystyle p\times q}
(
m
+
p
)
×
(
n
+
q
)
{\displaystyle (m+p)\times (n+q)}
[ 1]
A
⊕
B
=
(
A
0
0
B
)
=
(
a
11
⋯
a
1
n
0
⋯
0
⋮
⋱
⋮
⋮
⋱
⋮
a
m
1
⋯
a
m
n
0
⋯
0
0
⋯
0
b
11
⋯
b
1
q
⋮
⋱
⋮
⋮
⋱
⋮
0
⋯
0
b
p
1
⋯
b
p
q
)
{\displaystyle {\boldsymbol {A}}\oplus {\boldsymbol {B}}={\begin{pmatrix}{\boldsymbol {A}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {B}}\end{pmatrix}}={\begin{pmatrix}a_{11}&\cdots &a_{1n}&0&\cdots &0\\\vdots &\ddots &\vdots &\vdots &\ddots &\vdots \\a_{m1}&\cdots &a_{mn}&0&\cdots &0\\0&\cdots &0&b_{11}&\cdots &b_{1q}\\\vdots &\ddots &\vdots &\vdots &\ddots &\vdots \\0&\cdots &0&b_{p1}&\cdots &b_{pq}\end{pmatrix}}}
Například:
(
1
3
2
2
3
1
)
⊕
(
1
6
0
1
)
=
(
1
3
2
0
0
2
3
1
0
0
0
0
0
1
6
0
0
0
0
1
)
{\displaystyle {\begin{pmatrix}1&3&2\\2&3&1\end{pmatrix}}\oplus {\begin{pmatrix}1&6\\0&1\end{pmatrix}}={\begin{pmatrix}1&3&2&0&0\\2&3&1&0&0\\0&0&0&1&6\\0&0&0&0&1\end{pmatrix}}}
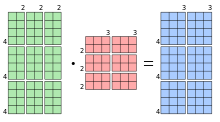
Ukázka součinu dvou blokových matic Součin vhodně rozdělených blokových matic lze určit z blokových podmatic. Má-li matice
A
{\displaystyle {\boldsymbol {A}}}
m
×
n
{\displaystyle m\times n}
A
=
(
A
11
A
12
⋯
A
1
r
A
21
A
22
⋯
A
2
r
⋮
⋮
⋱
⋮
A
q
1
A
q
2
⋯
A
q
r
)
{\displaystyle {\boldsymbol {A}}={\begin{pmatrix}{\boldsymbol {A}}_{11}&{\boldsymbol {A}}_{12}&\cdots &{\boldsymbol {A}}_{1r}\\{\boldsymbol {A}}_{21}&{\boldsymbol {A}}_{22}&\cdots &{\boldsymbol {A}}_{2r}\\\vdots &\vdots &\ddots &\vdots \\{\boldsymbol {A}}_{q1}&{\boldsymbol {A}}_{q2}&\cdots &{\boldsymbol {A}}_{qr}\end{pmatrix}}}
odpovídající rozkladům
m
=
m
1
+
m
2
+
⋯
+
m
q
{\displaystyle m=m_{1}+m_{2}+\cdots +m_{q}}
n
=
n
1
+
n
2
+
⋯
+
n
r
{\displaystyle n=n_{1}+n_{2}+\cdots +n_{r}}
B
{\displaystyle {\boldsymbol {B}}}
n
×
p
{\displaystyle n\times p}
B
=
(
B
11
B
12
⋯
B
1
s
B
21
B
22
⋯
B
2
s
⋮
⋮
⋱
⋮
B
r
1
B
r
2
⋯
B
r
s
)
,
{\displaystyle {\boldsymbol {B}}={\begin{pmatrix}{\boldsymbol {B}}_{11}&{\boldsymbol {B}}_{12}&\cdots &{\boldsymbol {B}}_{1s}\\{\boldsymbol {B}}_{21}&{\boldsymbol {B}}_{22}&\cdots &{\boldsymbol {B}}_{2s}\\\vdots &\vdots &\ddots &\vdots \\{\boldsymbol {B}}_{r1}&{\boldsymbol {B}}_{r2}&\cdots &{\boldsymbol {B}}_{rs}\end{pmatrix}},}
odpovídající rozkladům a
n
=
n
1
+
n
2
+
⋯
+
n
r
{\displaystyle n=n_{1}+n_{2}+\cdots +n_{r}}
p
=
p
1
+
p
2
+
⋯
+
p
s
{\displaystyle p=p_{1}+p_{2}+\cdots +p_{s}}
C
=
A
B
{\displaystyle {\boldsymbol {C}}={\boldsymbol {A}}{\boldsymbol {B}}}
je matice typu
m
×
p
{\displaystyle m\times p}
m
{\displaystyle m}
p
{\displaystyle p}
C
i
k
=
∑
j
=
1
r
A
i
j
B
j
k
.
{\displaystyle {\boldsymbol {C}}_{ik}=\sum _{j=1}^{r}{\boldsymbol {A}}_{ij}{\boldsymbol {B}}_{jk}.}
Nebo, vyjádřeno kompaktněji pomocí Einsteinovy sčítací konvence , která implicitně sčítá více existujících indexů
C
i
k
=
A
i
j
B
j
k
.
{\displaystyle {\boldsymbol {C}}_{ik}={\boldsymbol {A}}_{ij}{\boldsymbol {B}}_{jk}.}
Vhodné rozdělení matice na bloky a vztahy mezi nimi je základem rekurentního Strassenova algoritmu pro rychlý součin matic.
Bloková diagonální matice je čtvercová bloková matice, na jejíž hlavní úhlopříčce jsou čtvercové blokové matice a zbývající bloky jsou nulové matice . Bloková diagonální matice
A
{\displaystyle {\boldsymbol {A}}}
(
A
1
0
⋯
0
0
A
2
⋱
⋮
⋮
⋱
⋱
0
0
⋯
0
A
n
)
{\displaystyle {\begin{pmatrix}{\boldsymbol {A}}_{1}&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {A}}_{2}&\ddots &\vdots \\\vdots &\ddots &\ddots &{\boldsymbol {0}}\\{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}&{\boldsymbol {A}}_{n}\end{pmatrix}}}
kde podmatice
A
k
{\displaystyle {\boldsymbol {A}}_{k}}
A
{\displaystyle {\boldsymbol {A}}}
A
1
,
…
,
A
n
{\displaystyle {\boldsymbol {A}}_{1},\dotsc ,{\boldsymbol {A}}_{n}}
A
=
A
1
⊕
A
2
⊕
⋯
⊕
A
n
{\displaystyle {\boldsymbol {A}}={\boldsymbol {A}}_{1}\oplus {\boldsymbol {A}}_{2}\oplus \dotsb \oplus {\boldsymbol {A}}_{n}}
případně pomocí formalismu diagonálních matic
A
=
diag
(
A
1
,
A
2
,
…
,
A
n
)
{\displaystyle {\boldsymbol {A}}=\operatorname {diag} ({\boldsymbol {A}}_{1},{\boldsymbol {A}}_{2},\dotsc ,{\boldsymbol {A}}_{n})}
Pro determinant a stopu blokové diagonální matice platí
det
A
=
det
A
1
⋅
det
A
2
⋯
det
A
n
{\displaystyle \det {\boldsymbol {A}}=\det {\boldsymbol {A}}_{1}\cdot \det {\boldsymbol {A}}_{2}\dotsm \det {\boldsymbol {A}}_{n}}
a
tr
A
=
tr
A
1
+
⋯
+
tr
A
n
{\displaystyle \operatorname {tr} {\boldsymbol {A}}=\operatorname {tr} {\boldsymbol {A}}_{1}+\dotsb +\operatorname {tr} {\boldsymbol {A}}_{n}}
Inverzní matice k blokové diagonální matici
A
{\displaystyle {\boldsymbol {A}}}
(
A
1
0
⋯
0
0
A
2
⋱
⋮
⋮
⋱
⋱
0
0
⋯
0
A
n
)
−
1
=
(
A
1
−
1
0
⋯
0
0
A
2
−
1
⋱
⋮
⋮
⋱
⋱
0
0
⋯
0
A
n
−
1
)
.
{\displaystyle {\begin{pmatrix}{\boldsymbol {A}}_{1}&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {A}}_{2}&\ddots &\vdots \\\vdots &\ddots &\ddots &{\boldsymbol {0}}\\{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}&{\boldsymbol {A}}_{n}\end{pmatrix}}^{-1}={\begin{pmatrix}{\boldsymbol {A}}_{1}^{-1}&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {A}}_{2}^{-1}&\ddots &\vdots \\\vdots &\ddots &\ddots &{\boldsymbol {0}}\\{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}&{\boldsymbol {A}}_{n}^{-1}\end{pmatrix}}.}
Vlastní čísla blokové diagonální matice odpovídají sjednocení vlastních čísel blokových podmatic
A
1
,
A
2
,
…
,
A
n
{\displaystyle {\boldsymbol {A}}_{1},{\boldsymbol {A}}_{2},\dotsc ,{\boldsymbol {A}}_{n}}
Důležitým příkladem blokových diagonálních matic jsou matice v Jordanově normálním tvaru . V tomto případě jsou bloky takzvané Jordanovy bloky , což jsou bi-diagonální matice, jejichž hlavní úhlopříčka obsahuje vlastní číslo příslušné celému bloku, všechny prvky na vedlejší diagonále jsou 1, a ostatní prvky matice jsou nulové.
Bloková tridiagonální matice zobecňuje blokovou diagonální matice přidáním čtvercových blokových matic ve dvou prvních (horní a dolní) sekundárních diagonálách. Ostatní bloky jsou nulové matice. Bloková tridiagonální matice je v podstatě tridiagonální matice, ale s blokovými maticemi namísto skalárů . Bloková tridiagonální matice má tvar
(
B
1
C
1
0
⋯
0
A
2
B
2
C
2
0
⋱
⋱
⋱
⋱
⋮
A
k
B
k
C
k
⋮
⋱
⋱
⋱
⋱
0
A
n
−
1
B
n
−
1
C
n
−
1
0
⋯
0
A
n
B
n
)
{\displaystyle {\begin{pmatrix}{\boldsymbol {B}}_{1}&{\boldsymbol {C}}_{1}&{\boldsymbol {0}}&&\cdots &&{\boldsymbol {0}}\\{\boldsymbol {A}}_{2}&{\boldsymbol {B}}_{2}&{\boldsymbol {C}}_{2}&&&&\\{\boldsymbol {0}}&\ddots &\ddots &\ddots &\ddots &&\vdots \\&&{\boldsymbol {A}}_{k}&{\boldsymbol {B}}_{k}&{\boldsymbol {C}}_{k}&&\\\vdots &&\ddots &\ddots &\ddots &\ddots &{\boldsymbol {0}}\\&&&&{\boldsymbol {A}}_{n-1}&{\boldsymbol {B}}_{n-1}&{\boldsymbol {C}}_{n-1}\\{\boldsymbol {0}}&&\cdots &&{\boldsymbol {0}}&{\boldsymbol {A}}_{n}&{\boldsymbol {B}}_{n}\end{pmatrix}}}
přičemž
A
k
{\displaystyle {\boldsymbol {A}}_{k}}
B
k
{\displaystyle {\boldsymbol {B}}_{k}}
C
k
{\displaystyle {\boldsymbol {C}}_{k}}
Blokové tridiagonální matice se často objevují v numerických řešeních různých problémů (například ve výpočetní dynamice tekutin ). Existují optimalizované numerické metody pro LR rozklad blokových tridiagonálních matic a podobně účinné metody pro řešení soustav rovnic, jejichž matice je tridiagonální. Thomasův algoritmus, který se používá k efektivnímu řešení soustav rovnic s tridiagonální maticí, lze také použít pro blokové tridiagonální matice.
Bloková Toeplitzova matice je bloková matice, která podobně jako Toeplitzova matice obsahuje stejné bloky opakovaně na diagonále. Bloková Toeplitzova matice má tvar
(
A
(
1
,
1
)
A
(
1
,
2
)
⋯
A
(
1
,
n
−
1
)
A
(
1
,
n
)
A
(
2
,
1
)
A
(
1
,
1
)
A
(
1
,
2
)
A
(
1
,
n
−
1
)
⋱
⋱
⋱
⋮
A
(
2
,
1
)
A
(
1
,
1
)
A
(
1
,
2
)
⋮
⋱
⋱
⋱
A
(
n
−
1
,
1
)
A
(
2
,
1
)
A
(
1
,
1
)
A
(
1
,
2
)
A
(
n
,
1
)
A
(
n
−
1
,
1
)
⋯
A
(
2
,
1
)
A
(
1
,
1
)
)
.
{\displaystyle {\begin{pmatrix}{\boldsymbol {A}}_{(1,1)}&{\boldsymbol {A}}_{(1,2)}&&&\cdots &{\boldsymbol {A}}_{(1,n-1)}&{\boldsymbol {A}}_{(1,n)}\\{\boldsymbol {A}}_{(2,1)}&{\boldsymbol {A}}_{(1,1)}&{\boldsymbol {A}}_{(1,2)}&&&&{\boldsymbol {A}}_{(1,n-1)}\\&\ddots &\ddots &\ddots &&&\vdots \\&&{\boldsymbol {A}}_{(2,1)}&{\boldsymbol {A}}_{(1,1)}&{\boldsymbol {A}}_{(1,2)}&&\\\vdots &&&\ddots &\ddots &\ddots &\\{\boldsymbol {A}}_{(n-1,1)}&&&&{\boldsymbol {A}}_{(2,1)}&{\boldsymbol {A}}_{(1,1)}&{\boldsymbol {A}}_{(1,2)}\\{\boldsymbol {A}}_{(n,1)}&{\boldsymbol {A}}_{(n-1,1)}&\cdots &&&{\boldsymbol {A}}_{(2,1)}&{\boldsymbol {A}}_{(1,1)}\end{pmatrix}}.}
Bloková trojúhelníková matice je bloková analogie trojúhelníkové matice . Horní bloková trojúhelníková matice je čtvercová bloková matice, jejíž hlavní diagonála je tvořena čtvercovými blokovými maticemi a bloky nad hlavní diagonálou. Bloky pod hlavní diagonálou jsou nulové matice . Horní trojúhelníková bloková matice má tvar
(
A
11
A
12
⋯
A
1
n
0
A
22
⋱
⋮
⋮
⋱
⋱
A
n
−
1
,
n
0
⋯
0
A
n
n
)
,
{\displaystyle {\begin{pmatrix}{\boldsymbol {A}}_{11}&{\boldsymbol {A}}_{12}&\cdots &{\boldsymbol {A}}_{1n}\\{\boldsymbol {0}}&{\boldsymbol {A}}_{22}&\ddots &\vdots \\\vdots &\ddots &\ddots &{\boldsymbol {A}}_{n-1,n}\\{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}&{\boldsymbol {A}}_{nn}\end{pmatrix}},}
Analogicky je definována dolní trojúhelníková bloková matice.
Blokové trojúhelníkové matice hrají roli při rozhodování, zda je daná matice rozložitelná (redukovatelná) nebo nerozložitelná (neredukovatelná) . Matice
B
{\displaystyle {\boldsymbol {B}}}
rozložitelná, pokud existuje permutační matice
P
{\displaystyle {\boldsymbol {P}}}
P
B
P
T
{\displaystyle {\boldsymbol {P}}{\boldsymbol {B}}{\boldsymbol {P}}^{T}}
nerozložitelná (neredukovatelná) .
V tomto článku byl použit překlad textu z článku Blockmatrix
BÄRTSCH, Hans-Jochen. Matematické vzorce . Praha: Academia, 2006. 832 s. ISBN 80-200-1448-9 BEČVÁŘ, Jindřich. Lineární algebra . 1.. vyd. Praha: Matfyzpress, 2019. 436 s. ISBN 978-80-7378-392-1 HLADÍK, Milan. Lineární algebra (nejen) pro informatiky . 1.. vyd. Praha: Matfyzpress, 2019. 328 s. ISBN 978-80-7378-378-5 OLŠÁK, Petr. Lineární algebra [online]. Praha: 2007 [cit. 2023-02-20]. Dostupné online .