Gaussova kvadratura

Lichoběžníková metoda aproximuje funkci oranžovou čárkovanou úsečkou „Trap“, která spojuje funkční hodnoty na okrajích intervalu. Z obrázku je patrné, že tato aproximace není dobrá, takže chyba spočítané hodnoty integrálu je velká (lichoběžníková metoda dává hodnotu y(–1) + y(1) = –10, zatímco správná hodnota je 2/3). Aby se lichoběžníkovou metodou dosáhlo přesnějšího výsledku, bylo by nutné rozdělit integrační interval na mnoho podintervalů, funkci nahradit v každém podintervalu lineární funkcí a počítat mnoho funkčních hodnot funkce
Naproti tomu Gaussova metoda vybírá vhodnější body integrace, takže jediná lineární funkce (znázorněná černou čárkovanou úsečkou „Gauss 2“) aproximuje funkci mnohem lépe. Výsledek integrace dvoubodovou Gaussovou metodou je Tato hodnota je dokonce přesný výsledek, protože zelená oblast má stejnou plochu jako součet ploch červených oblastí. Důvodem je, že integrovaná funkce je ve skutečnosti polynom stupně 3, který je dvoubodovou Gaussovou kvadraturou aproximován přesně.
Numerické metody integrace jsou v numerické matematice metody výpočtu přibližných hodnot určitých integrálů funkcí. Při numerickém výpočtu určitého integrálu nějaké funkce se obvykle používá vážený součet hodnot této funkce v určitých bodech integračního intervalu – viz články Numerická integrace a Kvadratura (matematika).
Gaussova kvadratura, přesněji n-bodová Gaussova metoda numerické integrace, pojmenovaná po Carlu Friedrichu Gaussovi[1] je metoda numerické integrace, která díky vhodné volbě uzlů xi a vah wi pro i = 1, ..., n dává pro polynomy do stupně 2n − 1 přesné výsledky. Moderní formulaci, v níž se používají ortogonální polynomy vyvinul Carl Gustav Jacob Jacobi v roce 1826.[2] Nejobvyklejším integračním intervalem pro tuto metodu je , na kterém se pro výpočet určitého integrálu používá vzorec
který poskytuje přesné výsledky pro polynomy do stupně 2n − 1. Tato numerická metoda se nazývá Gaussova-Legendreova metoda numerické integrace. Metoda numerické integrace bude přesnou aproximací integrálu uvedeného výše pouze v případě, když funkci f(x) lze na intervalu dobře aproximovat polynomem stupně nejvýše 2n − 1.
Gaussova-Legendreova metoda numerické integrace se zpravidla nepoužívá pro integraci funkcí se singularitami v koncových bodech. V takovém případě se snažíme integrand zapsat jako
kde g(x) je funkce, kterou lze dobře aproximovat polynomem nízkého stupně. Pak použití alternativních uzlů a vah obvykle dává přesnější metody numerické integrace, které jsou známy jako Gaussova-Jacobiho kvadraturní pravidla:
Jako váhy se často používají hodnoty (Čebyševova–Gaussova kvadratura) a . Můžeme také chtít integrovat na intervalech neomezených z jedné (Gaussova-Laguerrova kvadratura) nebo obou stran (Gaussova–Hermitova kvadratura).
Lze ukázat (viz Press, et al. nebo Stoer a Bulirsch), že kvadraturní uzly xi jsou kořeny polynomu patřícího do třídy ortogonálních polynomů (třída ortogonální vůči váženému vnitřnímu součinu). To je klíčové pozorování pro výpočet uzlů a vah pro Gaussovu kvadraturu.
Gaussova–Legendreova kvadratura
[editovat | editovat zdroj]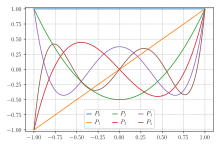
Pro nejjednodušší případ numerické integrace uvedený výše je funkce f(x) aproximována polynomy na intervalu a přidružené ortogonální polynomy jsou Legendreovy polynomy označované Pn(x). Zde je n-tý polynom normalizovaný tak, aby Pn(1) = 1, i-tý Gaussův uzel xi je i-tým kořenem polynomu Pn a váhy jsou dané vzorcem[3]
Integrační body a váhy pro Gaussovu–Legendreovu kvadraturu několika nižších řádů na intervalu jsou uvedeny v následující tabulce:
| Počet bodů, n | Body, xi | Váhy, wi | ||
|---|---|---|---|---|
| 1 | 0 | 2 | ||
| 2 | ±0.57735... | 1 | ||
| 3 | 0 | 0.888889... | ||
| ±0.774597... | 0.555556... | |||
| 4 | ±0.339981... | 0.652145... | ||
| ±0.861136... | 0.347855... | |||
| 5 | 0 | 0.568889... | ||
| ±0.538469... | 0.478629... | |||
| ±0.90618... | 0.236927... | |||
Jiné integrační intervaly
[editovat | editovat zdroj]Pro výpočet integrálu na obecném intervalu je třeba před použitím Gaussovy metody numerické integrace úlohu převést na integrál na intervalu pomocí vzorce
kde
Použití -bodového Gaussova kvadraturního pravidla pak dává následující aproximaci:
Příklad dvoubodového Gaussova kvadraturního pravidla
[editovat | editovat zdroj]Použijeme dvoubodovou Gaussovu metodu numerické integrace pro výpočet vzdálenosti, kterou uletí raketa v čase až s použitím vzorce
Změníme meze integračního intervalu, abychom mohli použít váhy a x-ové souřadnice uvedené v Tabulce 1. Také najdeme absolutní hodnotu relativní skutečné chyby. Přesný výsledek je 11061,34 metrů
Řešení:
provedeme změnu mezí integračního intervalu z na :
Použijeme váhy a hodnoty argumentu z Tabulky 1 pro dvoubodové pravidlo:
Načež můžeme použít Gaussův vzorec pro numerickou integraci
dostáváme
Pokud přesný výsledek je 11061,34 m, absolutní hodnota relativní skutečné chyby, je
Zobecnění
[editovat | editovat zdroj]Problém integrace lze vyjádřit poněkud obecnějším způsobem tak, že do integrandu vneseme kladnou váhovou funkci ω a povolíme jiné integrační intervaly než . Obecně tedy počítáme
pro určité a, b a ω. Pro a = −1, b = 1 a ω(x) = 1 jde o stejný problém, jaký je popsán výše. Jiné volby vedou k jiným integračním pravidlům, z nichž některá jsou tabelována níže. Čísla rovnic ve sloupci „A & S“ jsou podle Abramowitz a Stegun
| Interval | ω(x) | Ortogonální polynomy | A & S | Pro více informací, viz ... |
|---|---|---|---|---|
| 1 | Legendreovy polynomy | 25.4.29 | Gaussova–Legendreova kvadratura | |
| (−1, 1) | Jacobiho polynomy | 25.4.33 (β = 0) | Gaussova–Jacobiho kvadratura | |
| (−1, 1) | Čebyševovy polynomy (prvního druhu) | 25.4.38 | Čebyševova–Gaussova kvadratura | |
| Čebyševovy polynomy (druhého druhu) | 25.4.40 | Čebyševova–Gaussova kvadratura | ||
| Laguerrovy polynomy | 25.4.45 | Gaussova–Laguerre kvadratura | ||
| Zobecněné Laguerrovy polynomy | Gaussova–Laguerre kvadratura | |||
| Hermitovy polynomy | 25.4.46 | Gaussova–Hermitova kvadratura |
Základní věta
[editovat | editovat zdroj]Nechť pn je netriviální polynom stupně n, takový, že
Všimněte si, že toto bude splněno pro všechny ortogonální polynomy výše, protože každý polynom pn je zkonstruován tak, aby byl ortogonální k ostatním polynomům pj pro j<n, a xk je v rozsahu této množiny.
Pokud vybereme n uzlů xi tak, aby to byly kořeny polynomu pn, pak existuje n vah wi, pro které je integrál vypočítaný Gaussovou kvadraturou přesný pro všechny polynomy h(x) stupně nejvýše 2n − 1. Všechny tyto uzly xi budou navíc ležet v otevřeném intervalu (a, b)[4].
Pro důkaz první části tohoto tvrzení budeme předpokládat, že h(x) je jakýkoli polynom stupně nejvýše 2n − 1. Pokud jej vydělíme ortogonálním polynomem pn dostaneme
kde q(x) je podíl stupně nejvýše n − 1 (protože součet jeho stupně a stupně dělitele pn musí být roven stupni h(x)), a r(x) je zbytek také stupně nejvýše n − 1 (protože stupeň zbytku je vždy menší než stupeň dělitele). Protože pn je podle předpokladu ortogonální ke všem jednočlenům stupně menšího než n, musí být ortogonální také s podílem q(x). Proto
Protože zbytek r(x) má stupeň nejvýše n − 1, můžeme jej přesně interpolovat pomocí Lagrangeovy interpolace li(x) s n interpolačními body, kde
tedy
Jeho integrál pak bude roven
kde váha wi přiřazená uzlu xi je definována, aby vyrovnala vážený integrál li(x) (další vzorce pro váhy jsou uvedeny níže). Protože však všechny xi jsou kořeny polynomu pn, podle vzorce pro dělení uvedeného výše platí
pro všechna i. Tím dostáváme
Tím jsme dokázali, že pro jakýkoli polynom h(x) stupně nejvýše 2n − 1 je integrál přesně roven hodnotě spočítané Gaussovou kvadraturou.
Pro důkaz druhé části tvrzení použijeme polynom ve tvaru součinu kořenových činitelů pn. Komplexně sdružené kořeny tvoří kvadratické členy, které jsou na celé reálné ose buď kladné nebo záporné. Členy odpovídající kořenům ležícím mimo interval nemění na tomto intervalu znaménko. A členy odpovídající kořenům xi z intervalu které jsou liché násobnosti, násobí pn jedním dalším členem, který tvoří nový polynom
Tento polynom nemůže na intervalu měnit znaménko, protože všechny jeho kořeny mají sudou násobnost. Proto integrál
protože váhová funkce ω(x) je vždy nezáporná. Protože však pn je ortogonální ke všem polynomům stupně nejvýše n-1, bude stupeň součinu
alespoň n. Proto pn má n různých reálných kořenů v intervalu
Obecný vzorec pro váhy
[editovat | editovat zdroj]Váhy je možné vyjádřit vzorcem
|
|
(1) |
kde je koeficient u v . Pro důkaz je třeba si všimnout, že při použití Lagrangeovy interpolace můžeme r(x) vyjádřit pomocí jako
protože r(x) má stupeň menší než n a je proto určen hodnotami, kterých nabývá v n různých bodech. Když znásobíme obě strany ω(x) a zintegrujeme je na intervalu dostaneme
Váhy wi jsou tedy dány vzorcem
Tento integrální výraz pro lze vyjádřit pomocí ortogonálních polynomů a takto: Můžeme psát
kde je koeficient u v . Pokud se x limitně blíží dostaneme pomocí L'Hôpitalova pravidla
Můžeme tedy napsat výraz pro váhy s použitím integrálu ve tvaru
|
|
(2) |
Jmenovatel v integrandu můžeme zapsat
což dává
pokud , protože
je polynom stupně k − 1, který je tedy ortogonální k . Pokud tedy q(x) je polynom nejvýše n-tého stupně, můžeme napsat
Integrál na pravé straně můžeme pro vyhodnotit takto: Protože je polynom stupně n − 1, máme
kde s(x) je polynom stupně . Protože s(x) je ortogonální s platí
Pak můžeme psát
Člen v závorkách je polynom stupně , který je proto ortogonální s . Integrál tedy můžeme vyjádřit jako
Podle rovnice (2) se váhy získají vydělením tohoto výrazu výrazem , což dává výraz v rovnici (1).
Váhy mohou být také vyjádřeny pomocí ortogonálních polynomů a . V trojčlenném rekurentním vztahu bude mít člen s nulovou hodnotu, takže v (1) lze nahradit .
Důkaz, že váhy jsou kladné
[editovat | editovat zdroj]Uvažujme následující polynom stupně :
kde, jak je uvedeno výše, xj jsou kořeny polynomu . Je zřejmé, že . Protože stupeň je menší než , platí Gaussův vzorec pro numerickou integraci obsahující váhy a uzly získané z . Protože , pokud j není rovno i, máme
Protože jak tak jsou nezáporné funkce. Odtud plyne, že .
Numerická integrace Gaussovou metodou
[editovat | editovat zdroj]Existuje mnoho algoritmů pro výpočet uzlů xi a vah wi v Gaussově metodě numerické integrace. Nejoblíbenější jsou Golubův-Welschův algoritmus vyžadující O(n2) operací, Newtonova metoda pro řešení s pomocí trojčlenného rekurentního vztahu pro vyhodnocování, která vyžaduje O(n2) operací, a asymptotické vzorce pro velká n, které vyžadují O(n) operací.
Rekurentní vztah
[editovat | editovat zdroj]Ortogonální polynomy , pro které platí, že pro kde je skalární součin, stupeň a koeficient u nejvyššího členu je jedna (tj. jde o monické ortogonální polynomy) vyhovují rekurentnímu vztah
a skalární součin definovaný vzorcem
pro , kde n je nejvyšší stupeň, který může jít k nekonečnu, a kde . Především polynomy, definované rekurentním vztahem začínajícím , mají úvodní koeficient jedna a jsou správného stupně. Je-li dán počáteční bod , lze ortogonalitu dokázat indukcí. Pro máme
Pokud jsou ortogonální, pak také , protože ve výrazu
jsou všechny skalární součiny nulové kromě prvního a toho, kde je stejný ortogonální polynom. Proto
Pokud však pro skalární součin platí (což je v případě Gaussovy kvadratury splněno), rekurentní vztah lze zjednodušit na vztah obsahující tři členy: Pro je polynom stupně nejvýše r − 1. Na druhou stranu, je ortogonální ke každému polynomu stupně nejvýše r − 1. Proto máme a pro s < r − 1. Rekurentní vztah se pak zjednoduší na
nebo
(s konvencí ), kde
(poslední vztah platí, protože , protože se liší od ve stupni menším než r).
Golubův-Welschův algoritmus
[editovat | editovat zdroj]Trojčlenný rekurentní vztah lze zapsat v maticovém tvaru , kde , je -tý vektor standardní báze, tj. , a J je tak zvaná Jacobiho matice:
Nulové body polynomů do stupně n, které se používají jako uzly pro Gaussovu kvadraturu, lze nalézt výpočtem vlastních hodnot této třídiagonální matice. Tento postup je znám jako Golubův–Welschův algoritmus.
Pro výpočet vah a uzlů je vhodnější uvažovat symetrickou třídiagonální matici s prvky
J a jsou podobné matice a proto mají stejná vlastní čísla (uzly). Váhy lze vypočítat z odpovídajících vlastních vektorů: Pokud je normalizovaný vlastní vektor (tj. vlastní vektor s Eukleidovskou normou rovné jedné) příslušný k vlastní hodnotě xj, lze odpovídající váhu vypočítat z první složky tohoto vlastního vektoru, jmenovitě:
kde je integrál váhové funkce
Další detaily lze nalézt v monografii Numerical Methods for Special Function.[5]
Odhady chyby
[editovat | editovat zdroj]Pro integrand, který má 2n spojitých derivací, platí následující odhad chyby Gausovy metody numerické integrace:[6]
pro nějaké ξ z intervalu (a, b), kde pn je monický (tj. má úvodní koeficient roven 1) ortogonální polynom stupně n a kde
V důležitém speciálním případě, kdy ω(x) = 1, je odhad chyby:[7]
Tento odhad chyby může být v praxi problematický, protože odhad derivace řádu 2n může být obtížný, a skutečná chyba může být navíc mnohem menší než jakou dává tento odhad.[8] Alternativním přístupem může být použití dvou Gaussových metod numerické integrace s různými parametry, a odhadnutí chyby jako rozdílu obou výsledků. K tomuto účelu může být užitečná Gaussova–Kronrodova metoda numerické integrace.
Gaussova–Kronrodova pravidla
[editovat | editovat zdroj]Pokud bychom zjemnili rozdělení intervalu , Gaussovy body vyhodnocování na nových podintervalech se nebudou shodovat s předchozími body (až bodu nula pro liché n), a integrand by se tedy musel vyčíslovat v každém bodě. Gaussova–Kronrodova pravidla jsou rozšířením Gaussovy metody numerické integrace generované přidáním n + 1 bodů k n-bodovému pravidlu takovým způsobem, že výsledné pravidlo má řád 2n + 1 a umožňuje vypočítat odhady vyšších řádů s použitím funkčních hodnot z odhadů nižších řádů. Rozdíl mezi hodnotami získanými Gaussovou metodou numerické integrace a jejím Kronrodovým rozšířením se často používá pro odhad chyby aproximace.
Gaussova–Lobattova pravidla
[editovat | editovat zdroj]Metoda známá také jako Lobattova kvadratura[9] pojmenovaná po nizozemském matematikovi Rehuelu Lobattovi se podobá Gaussově kvadratuře s následujícími rozdíly:
- Integračními body jsou také koncové body integračního intervalu.
- Je přesná pro polynomy do stupně 2n – 3, kde n je počet integračních bodů[10].
Lobattova kvadratura funkce f(x) na intervalu :
X-ové souřadnice: xi je -tý kořen , zde označuje standardní Legendreův polynom m-tého stupeň a apostrof označuje derivaci.
Váhy:
Zbytek:
Integrační body a váhy pro několik nižších řádů jsou:
| Počet bodů, n | Body, xi | Váhy, wi |
|---|---|---|
Adaptivní varianta tohoto algoritmu se dvěma vnitřními uzly[11] je implementována v GNU Octave a MATLAB jako quadl a integrate.[12][13]
Odkazy
[editovat | editovat zdroj]Poznámky
[editovat | editovat zdroj]- ↑ GAUSS, Carl Friedrich. Methodus nova integralium valores per approximationem inveniendi. Comm. Soc. Sci. Göttingen Math. 1815, roč. 3, s. 29–76. Dostupné online. (latinsky)
- ↑ JACOBI, Carl Gustav Jacob. Ueber Gauß' neue Methode, die Werthe der Integrale näherungsweise zu finden. Journal für Reine und Angewandte Mathematik. 1826, roč. 1, s. 301–308,. Dostupné online. (německy)
- ↑ Abramowitz a Stegun 1983, p. 887.
- ↑ Stoer a Bulirsch 2002, s. 172–175.
- ↑ Gil, Segura a Temme 2007.
- ↑ Stoer a Bulirsch 2002, Thm 3.6.24.
- ↑ Kahaner, Moler a Nash 1989, §5.2.
- ↑ Stoer a Bulirsch 2002.
- ↑ Abramowitz a Stegun 1983, p. 888.
- ↑ Quarteroni, Sacco a Saleri 2000.
- ↑ GANDER, Walter; GAUTSCHI, Walter. Adaptive Quadrature - Revisited. BIT Numerical Mathematics. 2000, roč. 40, čís. 1, s. 84–101. Dostupné online. DOI 10.1023/A:1022318402393.
- ↑ Numerical integration - MATLAB integral [online]. Dostupné online.
- ↑ Functions of One Variable (GNU Octave) [online]. [cit. 2018-09-28]. Dostupné online.
Reference
[editovat | editovat zdroj]V tomto článku byl použit překlad textu z článku Gaussian quadrature na anglické Wikipedii.
- KABIR1, H.; MATIKOLAEI, S. A. H. H., 2017. Implementing an Accurate Generalized Gaussian Quadrature Solution to Find the Elastic Field in a Homogeneous Anisotropic Media. Journal of the Serbian Society for Computational Mechanics. Roč. 11, čís. 1, s. 11–19. Dostupné online. DOI 10.24874/jsscm.2017.11.01.02.
- ABRAMOWITZ, Milton; STEGUN, 1983 [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Svazek 55. Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. (Applied Mathematics Series). ISBN 978-0-486-61272-0.
- ANDERSON, Donald G., 1965. Gaussian quadrature formulae for. Math. Comp.. Roč. 19, čís. 91, s. 477–481. DOI 10.1090/s0025-5718-1965-0178569-1.
- GOLUB, Gene H.; WELSCH, John H., 1969. Calculation of Gauss Quadrature Rules. Mathematics of Computation. Roč. 23, čís. 106, s. 221–230. DOI 10.1090/S0025-5718-69-99647-1. JSTOR 2004418.
- GAUTSCHI, Walter, 1968. Construction of Gauss–Christoffel Quadrature Formulas. Math. Comp.. Roč. 22, čís. 102, s. 251–270. DOI 10.1090/S0025-5718-1968-0228171-0.
- GAUTSCHI, Walter, 1970. On the construction of Gaussian quadrature rules from modified moments. Math. Comp.. Roč. 24, s. 245–260. DOI 10.1090/S0025-5718-1970-0285117-6.
- PIESSENS, R., 1971. Gaussian quadrature formulas for the numerical integration of Bromwich's integral and the inversion of the laplace transform. J. Eng. Math.. Roč. 5, čís. 1, s. 1–9. DOI 10.1007/BF01535429. Bibcode 1971JEnMa...5....1P.
- DANLOY, Bernard, 1973. Numerical construction of Gaussian quadrature formulas forand. Math. Comp.. Roč. 27, čís. 124, s. 861–869. DOI 10.1090/S0025-5718-1973-0331730-X.
- KAHANER, David; MOLER, Cleve; NASH, Stephen, 1989. Numerical Methods and Software. [s.l.]: Prentice-Hall. Dostupné online. ISBN 978-0-13-627258-8.
- SAGAR, Robin P., 1991. A Gaussian quadrature for the calculation of generalized Fermi-Dirac integrals. Comput. Phys. Commun.. Roč. 66, čís. 2–3, s. 271–275. DOI 10.1016/0010-4655(91)90076-W. Bibcode 1991CoPhC..66..271S.
- YAKIMIW, E., 1996. Accurate computation of weights in classical Gauss-Christoffel quadrature rules. J. Comput. Phys.. Roč. 129, čís. 2, s. 406–430. DOI 10.1006/jcph.1996.0258. Bibcode 1996JCoPh.129..406Y.
- LAURIE, Dirk P., 1999. Accurate recovery of recursion coefficients from Gaussian quadrature formulas. J. Comput. Appl. Math.. Roč. 112, čís. 1–2, s. 165–180. DOI 10.1016/S0377-0427(99)00228-9.
- LAURIE, Dirk P., 2001. Computation of Gauss-type quadrature formulas. J. Comput. Appl. Math.. Roč. 127, čís. 1–2, s. 201–217. DOI 10.1016/S0377-0427(00)00506-9. Bibcode 2001JCoAM.127..201L.
- RIENER, Cordian; SCHWEIGHOFER, Markus, 2018. Optimization approaches to quadrature: New characterizations of Gaussian quadrature on the line and quadrature with few nodes on plane algebraic curves, on the plane and in higher dimensions. Journal of Complexity. Roč. 45, s. 22–54. DOI 10.1016/j.jco.2017.10.002. arXiv 1607.08404.
- STOER, Josef; BULIRSCH, Roland, 2002. Introduction to Numerical Analysis. 2. vyd. [s.l.]: Springer. Dostupné online. ISBN 978-0-387-95452-3..
- TEMME, Nico M., 2010. NIST Handbook of Mathematical Functions. Příprava vydání in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W.. [s.l.]: Cambridge University Press. ISBN 978-0-521-19225-5.
- PRESS, WH; TEUKOLSKY, SA; VETTERLING, WT; FLANNERY, BP, 2007. Numerical Recipes: The Art of Scientific Computing. 2. vyd. New York: Cambridge University Press. ISBN 978-0-521-88068-8. Kapitola Section 4.6. Gaussian Quadratures and Orthogonal Polynomials.
- GIL, Amparo; SEGURA, Javier; TEMME, Nico M., 2007. Numerical Methods for Special Functions. [s.l.]: SIAM. ISBN 978-0-89871-634-4. Kapitola §5.3: Gauss quadrature.
- QUARTERONI, Alfio; SACCO, Riccardo; SALERI, Fausto. Numerical Mathematics. New York: Springer-Verlag, 2000. ISBN 0-387-98959-5. S. 422, 425.
- GAUTSCHI, Walter. A Software Repository for Gaussian Quadratures and Christoffel Functions. [s.l.]: SIAM, 2000. ISBN 978-1-611976-34-2.
- LAUDADIO, Teresa; MASTRONARDI, Nicola; VAN DOOREN, Paul, 2023. Computing Gaussian quadrature rules with high relative accuracy. Numerical Algorithms. Roč. 92, s. 767–793.
Související články
[editovat | editovat zdroj]Literatura
[editovat | editovat zdroj]- SEGETHOVÁ, J. Základy numerické matematiky. Praha: MFF UK, 2002.
Externí odkazy
[editovat | editovat zdroj]- Gauss quadrature formula Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- ALGLIB obsahuje sadu algoritmů pro numerickou integration (v jazycích C# / C++ / Delphi / Visual Basic / atd.)
- GNU Scientific Library — obsahuje implementaci algoritmů QUADPACK pro programovací jazyk C (viz též GNU Scientific Library)
- From Lobatto Quadrature to the Euler constant e
- Gaussian Quadrature Rule of Integration – Notes, PPT, Matlab, Mathematica, Maple, Mathcad at Holistic Numerical Methods Institute
- Gaussova kvadratura v encyklopedii MathWorld (anglicky)
- Gaussian Quadrature autoři: Chris Maes a Anton Antonov, Wolfram Demonstrations Project.
- Tabulované váhy a uzly zdrojovým kódem pro systém Mathematica, high přesností (16 a 256 desítkových míst) Legendreova-Gaussovy kvadraturní váhy a uzly, pro n=2 through n=64, zdrojovým kódem pro systém Mathematica.
- Mathematica source code distributed under the GNU LGPL pro generování uzlů vah pro libovolné váhové funkce W(x), integrační intervaly a přesnosti.
- Gaussova kvadratura v Boost.Math, pro libovolnou přesnost a řád aproximace
- Gaussova-Kronrodova kvadratura v Boost.Math
- Uzly a váhy pro Gaussovu kvadraturu Archivováno 14. 4. 2021 na Wayback Machine.















![{\displaystyle w_{i}={\frac {2}{\left(1-x_{i}^{2}\right)\left[P'_{n}(x_{i})\right]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a5533b3b5d42f1c60c3c5e6e5d62c37c2878a3)





















![{\displaystyle x=\int _{8}^{30}{\left(2000\ln \left[{\frac {140000}{140000-2100t}}\right]-9.8t\right){dt}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecae0be1e93272d4b632f12789948635659cd3f5)







![{\displaystyle {\begin{aligned}11\int _{-1}^{1}{f\left(11x+19\right){dx}}&\approx 11\left[c_{1}f\left(11x_{1}+19\right)+c_{2}f\left(11x_{2}+19\right)\right]\\&=11\left[f\left(11(-0.5773503)+19\right)+f\left(11(0.5773503)+19\right)\right]\\&=11\left[f(12.64915)+f(25.35085)\right]\\&=11\left[(296.8317)+(708.4811)\right]\\&=11058.44\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1cb61ab73cc8da5361e4b92d7767b1096d61ab1)
![{\displaystyle {\begin{aligned}f(12.64915)&=2000\ln \left[{\frac {140000}{140000-2100(12.64915)}}\right]-9.8(12.64915)\\&=296.8317\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35daceca417b58a97f96c064305ec13426bb40d8)
![{\displaystyle {\begin{aligned}f(25.35085)&=2000\ln \left[{\frac {140000}{140000-2100(25.35085)}}\right]-9.8(25.35085)\\&=708.4811\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3433f0d527732886cba3d09aa9733423abc8628f)
















































































































![{\displaystyle {\frac {\left(b-a\right)^{2n+1}\left(n!\right)^{4}}{(2n+1)\left[\left(2n\right)!\right]^{3}}}f^{(2n)}(\xi ),\qquad a<\xi <b.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55978744de6e75175beed299cc41fd11d8cdddc9)
![{\displaystyle \int _{-1}^{1}{f(x)\,dx}={\frac {2}{n(n-1)}}[f(1)+f(-1)]+\sum _{i=2}^{n-1}{w_{i}f(x_{i})}+R_{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/debe72ac248f8ae18af6b8814511b7068487ba24)



![{\displaystyle w_{i}={\frac {2}{n(n-1)\left[P_{n-1}\left(x_{i}\right)\right]^{2}}},\qquad x_{i}\neq \pm 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef48203f09833d6a365e378e786320cbca4938f7)
![{\displaystyle R_{n}={\frac {-n\left(n-1\right)^{3}2^{2n-1}\left[\left(n-2\right)!\right]^{4}}{(2n-1)\left[\left(2n-2\right)!\right]^{3}}}f^{(2n-2)}(\xi ),\qquad -1<\xi <1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3958e99104629c7d8c85c193a735f2ddea4652db)





























