Superpermutace

Distribuce permutací v superpermutaci tří prvků

Superpermutace jsou pojmem kombinatoriky, kde superpermutace $n$ symbolů je řetězcem obsahujícím každou permutaci těchto $n$ symbolů ve formě podřetězce. Triviálně může být superpermutace složena prostým spojením všech řetězců jednotlivých permutací. Krom triviálního případu $n=1$ lze najít řetězec kratší, poněvadž se tyto podřetězce mohou překrývat. Příkladně – pro $n=2$ existuje superpermutace $1221$, která obsahuje obě permutace, tj. $12$ a $21$. Existuje ovšem i kratší řetězec $121$, jenž je obsahuje také.

Bylo dokázáno, že nejkratší superpermutace $n$ symbolů pro $1\leq n\leq 5$ má délku $1!+2!+\dots +n!$ Pro 1–4 znaky mají superpermutace délky 1, 3, 9 a 33. Samotné superpermutace poté mají podobu $1$, $121$, $123121321$ a $12341231$$42312431$$21342132$$413214321$. Pro $n=5$ existuje několik známých superpermutací o délce 153 znaků, jedna taková je ukázána níže. Odlišná superpermutace by šla vytvořit prohozením všech čtyřek a pětek v druhé polovině (po tučně označeném písmenu 2):

$12345123$$41523412$$53412354$$12314523$$14253142$$35142315$$42312453$$12435124$$31524312$$5431\mathbf {2} 134$$52134251$$34215342$$13542132$$45132415$$32413524$$13254132$$14532143$$52143251$$432154321$.

Pro $n>5$ zatím nebyl nalezen jednoznačný vztah, pomocí kterého by šlo superpermutaci přímo hledat, jsme ovšem schopni spočíst spodní a horní mez intervalu, ve kterém se délka superpermutace nachází.

Hledání superpermutací

Diagram vytváření superpermutace 3 symbolů ze superpermutace 2 symbolů

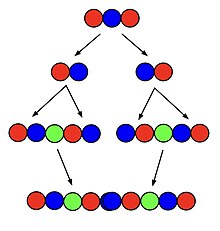
Jeden z nejběžnějších algoritmů hledání superpermutace řádu $n$ je algoritmus rekurzivní. V prvním kroku rozdělíme superpermutaci $n-1$ prvků do svých permutací seřazených podle toho, v jakém pořadí se vyskytují v superpermutaci. Každá z těchto permutací je následně umístěna vedle kopie sebe samé, přičemž mezi obě kopie je přidán symbol $n$. Nakonec jsou všechny vzniklé struktury umístěny vedle sebe a všechny sousední identické symboly jsou sloučeny.

Například superpermutace třetího řádu může být vytvořena z jiné se dvěma symboly. Začneme se superpermutací $121$ a rozdělíme ji na permutace $12$ a $21$. Vytvoříme kopie a přidáme další symbol, čímž vzniknou řetězce $12312$ a $21321$. Ty spojíme, čímž následně vznikne $1231221321$. Redundantní opakované dvojky uprostřed se můžeme zbavit, čímž vznikne kratší řetězec $123121321$, jenž je optimální superpermutací řádu 3. Tímto algoritmem jsme schopni vytvořit optimální superpermutace pro každé $n\leq 5$, pro vyšší $n$ algoritmus není platný a jím vytvořené superpermutace mají od těch optimálních daleko.

Superpermutace můžeme hledat i přes vytvoření grafu, kde každá permutace je vrcholem spojeným hranou. Každá hrana má váhu, váha je zde určována dle počtu znaků, které můžeme přidat na konec permutace (vypustit stejný počet znaků z počátku), abychom získali další permutaci. Ku příkladu, hrana mezi permutacemi $123$ a $312$ má váhu 2, protože $123+12=12312=312$. Každá hamiltonovská kružnice vedená tímto grafem je superpermutací, problém hledání cesty s nejmenší vahou zde nabývá formy problému obchodního cestujícího. První nalezená superpermutace s délkou kratší než $1!+2!+\ldots +n!$ byla získána právě přes počítačové vyhledávání informatikem Robinem Houstonem.

Dolní meze, téže problém Haruhi

Dne 27. září 2011 neznámý příspěvatel na nástěnku „Science & Math“ (Věda a matematika) Imageboard fóra 4chan zveřejnil důkaz o délce nejkratší superpermutace $n$ symbolů pro $n\geq 2$. Ta má délku alespoň $n!+(n-1)!+(n-2)!+n-3$. Občas je nazýván dle japonského animovaného seriálu Haruhi, který používá techniku nelineárního vypravování – uživatelé tohoto fóra si položili otázku, kolik nejméně episod by museli zhlédnout, aby viděli všech 14 episod v každém možném pořadí. . Do hledáčku veřejnosti se důkaz dostal v roce 2018 poté, co Robin Houston o důkazu napsal příspěvek na síť Twitter. Dne 25. října 2018 Robin Houston, Jay Pantone a Vince Vatter publikovali formaliovanou verzi důkazu na Online encyklopedii celočíselných sekvencí Zveřejněná forma tohoto článku, připisována „Anonymnímu příspěvateli fóra 4chan“ se objevila v American Mathematical Monthly.

Specificky pro „problém Haruhi“ (14 episod, tj. 14 symbolů) jsou aktuálně nejlepší známé spodní, respektive horní meze 93 884 313 611, resp. 93 924 230 411. Při průměrné délce episody to znamená, že zhlédnout všechny episody ve všech možných pořadích by trvalo zhruba 4,3 milionu let.

Horní meze

Dne 20. října 2018 sestrojil autor science fiction a matematik Greg Egan algoritmus pro hledání superpermutačních řetězců délky $n!+(n-1)!+(n-2)!+(n-3)!+n-3$. přizpůsobením konstrukce Aarona Williamse pro vytváření hamiltonovských kružnic skrze Cayleyův graf symetrické grupy. V té době šlo o nejkratší známé superpermutační řetězce pro $n\geq 7$. Dne 1. února 2019 Bogdan Coanda oznámil, že pro $n=7$ našel superpermutační řetězec délky 5907, což je ekvivalentní s $(n!+(n-1)!+(n-2)!+(n-3)!+n-3)-1$, šlo tedy o nový rekord. Dne 27. února 2019, využívaje myšlenky vyvinuté Robinem Houstonem, Egan pro $n=7$ nalezl superpermutační řetězec o délce 5906. Zda existují podobné kratší superpermutační řetězce pro hodnoty $n>7$, zůstává nevyřešenou otázkou. Aktuální nejlepší známou dolní mezí (vizte výše uvedenou sekci) pro $n=7$ je stále 5884.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Superpermutation na anglické Wikipedii.

Literatura

• ASHLOCK, Daniel A.; TILLOTSON, Jenett. Construction of small superpermutations and minimal injective superstrings. Congressus Numerantium. 1993, s. 91–98. 
• ((ANONYMOUS 4CHAN POSTER)); HOUSTON, Robin; PANTONE, Jay; VATTER, Vince. A lower bound on the length of the shortest superpattern. On-Line Encyclopedia of Integer Sequences. October 25, 2018. Dostupné online. 

Související články

• De Bruijnova posloupnost, podobný problém s cyklickými řadami

Externí odkazy

• The Minimal Superpermutation Problem – Nathaniel Johnston's blog
• GRIME, James. Superpermutations - Numberphile [online]. Brady Haran [cit. 2018-02-01]. Dostupné online. 
• The original 4chan post on /sci/, archivováno na warosu.org
• Tweet Robina Houstona, který zviditelnil příspěvek na diskusním fóru 4chan
• Článek o hledání krátkých superpermutacích v magazínu Quanta
• Štěpán Holub – Kombinatorika na slovech
• BANNERJEE, Ritam. The Melancholy Of Haruhi Suzumiya Watch Order Explained! [online]. Rev. 2022-04-09 [cit. 2025-02-21]. Dostupné online. (anglicky)