Rovina
Rovina je v matematice dvourozměrný geometrický útvar, který si lze představit jako neomezenou dokonale rovnou plochu. Algebraicky vyjádřeno, jde o množinu bodů izomorfní s dvoudimenzionálním lineárním prostorem. Jinak řečeno jde o dvoudimenzionální afinní prostor.
Rovina může být určena třemi různými body, nebo přímkou a bodem, který leží mimo tuto přímku.
Značení
[editovat | editovat zdroj]Rovina je buď plocha, na kterou se kreslí (nákresna), nebo se znázorňuje některým rovinným útvarem pomocí některého geometrických promítání. Rovina se označuje malým řeckým písmenem.
Znázornění:
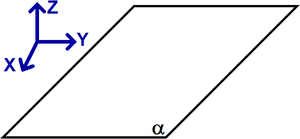
Rovnice roviny
[editovat | editovat zdroj]Rovina je množina bodů prostoru, které vyhovují tzv. rovnici roviny, která může být zadána v různých tvarech.
Obecná rovnice roviny
[editovat | editovat zdroj]Obecná rovnice roviny má tvar
- ,
kde koeficienty nejsou současně nulové a jsou to koeficienty normálového vektoru roviny (vektoru kolmého k rovině). Proměnné jsou souřadnice bodu ležícího v rovině.
V případě, že známe tři body určující rovinu, obecnou rovnici roviny získáme takto: spočteme vektory a , vypočítáme jejich Vektorový součin ze kterého získáme koeficienty a napíšeme obecnou rovnici. Zbývající koeficient d získáme tak, že dosadíme souřadnice bodu K (nebo kteréhokoli jiného bodu ze zadání) do napsané rovnice.
Parametrické vyjádření roviny
[editovat | editovat zdroj]Parametrické vyjádření roviny má například vektorový tvar , který se dá rozepsat dle složek takto:
- ,
kde a je bod, který leží v rovině a vektory a jsou nekolineární vektory ležící v rovině, tzn. jsou to směrové vektory roviny.
Úseková rovnice roviny
[editovat | editovat zdroj]Úsekovou rovnici roviny zapisujeme jako
- ,
kde vymezují úseky vyťaté rovinou na osách .
Srovnáním úsekové a obecné rovnice dostáváme .
Normálová rovnice roviny
[editovat | editovat zdroj]Normálová rovnice roviny má tvar
- ,
kde je vzdálenost počátku souřadného systému od roviny, tj. délka normály od počátku souřadnicového systému do průsečíku s rovinou,
jsou směrové kosiny roviny,
představují úhly, které svírají kladné souřadnicové poloosy s normálou roviny.
Normála je směrnice kolmá ve všech směrech k rovině.
Směrové kosiny lze vyjádřit z obecné rovnice jako
kde pro a pro pro .
Rovinný řez
[editovat | editovat zdroj]Rovinným řezem geometrického útvaru rovinou se nazývá průnik roviny a útvaru .
Rovinný řez plochy rovinou, ve které leží normála plochy, se nazývá normálovým řezem plochy.
Další informace
[editovat | editovat zdroj]V mechanice a technice existují rovinné úlohy, tj. jestliže lze idealizovat těleso či technikou konstrukci tak, že leží a v jedné rovině. V této rovině také působí všechna zatížení. Příkladem mohou být např. rovinné příhradové konstrukce, rovinný ohyb nebo úlohy rovinné napjatosti či rovinné deformace.
Literatura
[editovat | editovat zdroj]- Marcela Palková a kolektiv: Průvodce matematikou 2, Didaktis, Brno 2007, ISBN 978-80-7358-083-4, str. 107-109
Související články
[editovat | editovat zdroj]- Geometrie
- Základní geometrické útvary
- Polorovina
- Vzájemná poloha bodu a roviny
- Vzájemná poloha rovin
- Vzájemná poloha přímky a roviny































