Středová souměrnost
Středová souměrnost je typ geometrického zobrazení v afinním prostoru.
V euklidovském prostoru středová souměrnost zachovává vzdálenosti i úhly, jedná se tedy o shodnost.
Definice
[editovat | editovat zdroj]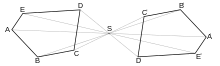
Středová souměrnost na přímce, v rovině nebo v obecném (afinním) prostoru se středem v bodě (tzv. střed souměrnosti) je takové zobrazení, které zobrazuje střed na sebe sama a bod různý od na bod , který se nachází na polopřímce opačné k ve stejné vzdálenosti od jako bod (tj. platí pro něj ).
Objekt (ať již na přímce, v rovině nebo v prostoru) označujeme za středově souměrný, pokud je v nějaké středové souměrnosti obrazem sebe sama. Střed této středové souměrnosti pak nazýváme středem souměrnosti objektu.
Středová souměrnost v prostoru se středem v počátku souřadné soustavy se též nazývá prostorová inverze, užívá se v teoretické fyzice.
Příklady
[editovat | editovat zdroj]
- Úsečka nebo sjednocení dvou úseček stejné délky je příkladem středově souměrných objektů na přímce.
- Naproti tomu žádná polopřímka není na přímce středově souměrná.
- Obdélník, čtverec, kosočtverec, pravidelný šestiúhelník nebo kruh jsou příklady středově souměrných obrazců v rovině.
- Naproti tomu žádný mnohoúhelník s lichým počtem vrcholů (tedy například žádný trojúhelník) nemůže být středově souměrný.
- Hyperbola a elipsa jsou dalšími příklady středově souměrných rovinných útvarů, zatímco parabola středově souměrná není.
- Krychle, koule nebo rotační válec jsou příkladem středově souměrného prostorového útvaru.
- Naproti tomu žádný jehlan ani kužel nemůže být středově souměrný.
Vlastnosti
[editovat | editovat zdroj]Středová souměrnost s pevně daným středem je sama sobě inverzním zobrazením - složením dvou středových souměrností se stejným středem vzniká identita.
Kromě vzdáleností zachovává středová souměrnost v rovině i orientaci - pokud bylo pořadí vrcholů v trojúhelníku po směru hodinových ručiček, pak pořadí jejich obrazů ve středové souměrnosti je opět po směru hodinových ručiček (což je něco, co neplatí například pro osovou souměrnost).
Středová souměrnost se středem v bodě je v rovině shodná s otočením o 180 stupňů podle středu . Trochu jiná je situace v prostoru, kde nemá smysl mluvit o otočení kolem bodu, ale kolem osy.
Středová souměrnost je involucí, neboť bod je samodružný a každá přímka procházející tímto bodem je také samodružná.
Literatura
[editovat | editovat zdroj]- POMYKALOVÁ E. a kol., 2010: Matematika pro gymnázia - Stereometrie. Praha: Prometheus.
- BOČEK L., KOČANDRLE M., SEKANINA M., ŠEDIVÝ J., 1980. Geometrie II. Praha: SPN.
Související články
[editovat | editovat zdroj]Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu středová souměrnost na Wikimedia Commons
Obrázky, zvuky či videa k tématu středová souměrnost na Wikimedia Commons





