Problém byzantských generálů
Problém byzantské shody,[1] problém interaktivní konzistence, problém zdrojové kongruence, chybová lavina nebo byzantské selhání jsou označení pro problém distribuovaného systému, jehož komponenty mohou selhat, přičemž nejsou dokonalé informace o tom, které komponenty selhaly. Vadné komponenty mohou narušovat činnost systému zasíláním nepravdivých zpráv.
K této situaci může dojít, pokud u jedné nebo více komponent dojde k byzantské poruše, při které se daná komponenta může některým systémům detekce selhání jevit jako vadná a jiným jako fungující. Pro ostatní komponenty je proto obtížné ji prohlásit za vadnou a odpojit od sítě, protože potřebují nejdříve dosáhnout konsenzu, která komponenta selhala. Odolnost proti byzantským poruchám (anglicky Byzantine fault tolerance, BFT) je odolnost počítačového systému proti chybám na takové situace.
Pro ilustraci uvedené situace byla vytvořena alegorie nazývaná „problém byzantských generálů“,[2] kdy se několik aktérů musí dohodnout na koordinované strategii, aby zabránili katastrofickému selhání systému, ale někteří z těchto aktérů jsou nespolehliví:
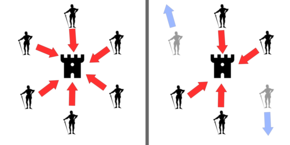
Uvažujme několik generálů, kteří se svými jednotkami chtějí společně dobýt pevnost. Generálové musí rozhodnout jako skupina, zda společný útok provést nebo ne; někteří mohou dávat přednost útoku, zatímco ostatní ústupu. Je třeba, aby se všichni generálové dohodli na společném postupu, protože polovičatý útok části jednotek by byl odražen, a byl by horší než provedení společného útoku nebo se koordinovaný ústup.
Problém komplikuje přítomnost zrádných generálů, kteří mohou nejen hlasovat pro neoptimální strategii, ale mohou to dělat selektivně. Pokud například devět generálů bude hlasovat, čtyři z nich podporují útok, zatímco čtyři ostatní jsou pro ústup, devátý generál může poslat hlas pro ustoupit těm generálům, kteří jsou pro ústup, a hlas pro útok zbytku. Ti, kdo od devátého generála přijali hlas ustoupit, ustoupí, zatímco zbytek bude útočit (což způsobí selhání útoku). Problém je dále komplikován tím, že generálové jsou fyzicky odděleni a musí posílat své hlasy prostřednictvím poslů, kterým se nemusí podařit hlasy doručit, nebo mohou podvrhnout falešné hlasy.
Definice
[editovat | editovat zdroj]Byzantská porucha je libovolná porucha, která ukazuje různé symptomy různým pozorovatelům.[3] Byzantské selhání je narušení služeb systému kvůli byzantské poruše v systémech, které vyžadují konsenzus mezi distribuovanými uzly.[4]
Odolnost proti byzantským poruchám lze dosáhnout, pokud mezi loajálními generály (tj. těmi, kteří netrpí poruchou) panuje většinová shoda o strategii. Chybějícím zprávám může být dána implicitní hodnota hlasu. Chybějícím zprávám může být například dána “nulová“ hodnota. Dále, Pokud je shoda, že nulové hlasy jsou ve většině, předpřiřazená implicitní strategie může být použita (například ústup).[5]
Typickým mapováním tohoto příběhu na počítačové systémy je, že počítače jsou generálové a jejich komunikační spoje jsou poslové. Ačkoli problém je formulována jako analogie rozhodování a problému datové bezpečnosti, v elektronice nemůže být vyřešen pouze kryptografickými digitálními podpisy, protože závady jako je nesprávné napětí se mohou šířit procesem šifrování. Určitá komponenta se tedy může jevit jako fungující další komponentě a jako vadná jiné komponentě, což brání dosažení shody v otázce, zda je první komponenta vadná nebo ne.[3]
Formální definice:
Je dán systém n komponent, z nichž t je vadných (odpovídajících zrádným, nepoctivým generálům), a mezi všemi komponentami vedou pouze dvoubodové komunikační kanály.[6]
Kdykoli se komponenta A pokusí vyslat hodnotu x, ostatní komponenty mohou vzájemně diskutovat a ověřovat konzistenci vysílání komponenty A, a nakonec se shodnout na společné hodnotě y.
Řekneme, že systém odolává byzantskému selhání, pokud komponenta A může vysílat hodnotu x, tak že:
- Pokud A je poctivá, pak se všechny poctivé komponenty dohodnou na hodnotě x.
- V každém případě se všechny poctivé komponenty shodnou na stejné hodnotě y.
Problém byl studován jak pro synchronní tak pro asynchronní komunikaci.
Předpokládá se, že výše uvedený komunikační graf je úplným grafem (tj. každá komponenta může komunikovat s každou jinou), ale komunikační graf nemusí být úplný.
Úloha může být také rozvolněna na „realističtější“ problém, kde se nepoctivé komponenty spolu nedomlouvají, aby svedly ostatní k chybě. Právě pro tento případ byly navrženy praktické algoritmy.
Historie
[editovat | editovat zdroj]Problém dosažení byzantského konsensu formuloval a formalizoval Robert Shostak, který jej nazval problémem interaktivní konzistence. Tuto práci uskutečnil v roce 1978 v rámci projektu SIFT sponzorovaného NASA[7] v laboratoři počítačových věd společnosti SRI International. SIFT (Software Implemented Fault Tolerance) byl dítětem Johna Wensleyho, a byl založen na myšlence použití více univerzálních počítačů, které by spolu komunikovaly prostřednictvím párovaných zpráv, aby dosáhly shody, i když by některé z počítačů byly vadné.
Na začátku projektu nebylo jasné, kolik počítačů bude celkem potřeba, aby bylo zaručeno, že spiknutí n vadných počítačů nemůže „zmařit“ úsilí správně fungujících počítačů o dosažení shody. Shostak ukázal, že je jich potřeba nejméně 3n+1, a navrhl dvoukolový protokol 3n+1 pro zasílání zpráv, který by fungoval pro n=1. Jeho kolega Marshall Pease zobecnil algoritmus pro libovolné n > 0, a dokázal, že 3n+1 je jak nezbytné tak dostačující. Tyto výsledky, spolu s pozdějším důkazem dostatečnosti 3n při použití digitálních podpisů od Leslie Lamporta, byly publikovány v zásadním článku, Reaching Agreement in the Presence of Faults (Dosažení shody v přítomnosti selhání.)[8] Autoři získali za tento článek v roce 2005 cenu Edsgera W. Dijkstry.
Pro snazší porozumění problému interaktivní konzistence vymyslel Lamport barvitou alegorii, v níž skupina armádních generálů připravuje plán útoku na město. Původní verze příběhu byla o velitelích albánské armády. Na návrh Jacka Goldberga byl název změněn, aby se někdo nemohl cítit uražen a nakonec se ustálil na „byzantských generálech“.[9] Stejní autoři prezentovali tuto formulaci problému spolu s některými dalšími výsledky v roce 1982 ve článku „Problém byzantských generálů“ (anglicky The Byzantine Generals Problem).[5]
Přístup k řešení
[editovat | editovat zdroj]Účelová funkce odolnosti proti byzantskému selhání je schopna bránit proti chybám komponent systému se symptomy nebo bez symptomů, které brání jiným komponentám systému dosáhnout vzájemné shody, kde taková shoda je potřebná pro správné fungování systému.
Zbývající správně fungující komponenty systému odolného proti byzantskému selhání budou schopny pokračovat v poskytování požadovaných služeb systému, předpokládá existenci dostačujícího počtu korektně fungujících komponent pro zachování služby.
Byzantská selhání jsou považována za nejobecnější a nejobtížnější třídu chyb mezi příčinami selhání. Zastavení při selhání (anglicky fail-stop) je naopak nejjednodušší třídou chyb. Předpokládá, že uzel, který selže, prostě přestane fungovat, což mohou ostatní uzly snadno detekovat. Naproti tomu byzantská selhání nemají žádná omezení, což znamená, že vadný uzel může generovat libovolná data, včetně dat, která vypadají jako od funkčního uzlu. Byzantská selhání tedy mohou mást systémy detekce selhání, kvůli čemuž je obtížné dosáhnout odolnosti proti selhání. Bez ohledu na analogii, byzantské selhání nemusí být bezpečnostním problémem, na kterém se podílí nepřátelské lidské rozhraní: může se jednat o čistě elektrické nebo softwarové selhání.
Termín porucha/závada (anglicky fault) a selhání (anglicky failure) se zde používají podle standardní definice,[10] které vytvořila společná komise pro „Základní koncepty a terminologii“ založená technickým výborem IEEE Computer Society pro spolehlivou výpočetní techniku a odolnost proti poruchám a pracovní skupinou IFIP 10.4 pro spolehlivou výpočetní techniku a odolnost proti poruchám.[11] Viz také dependability.
Odolnost proti byzantským selháním se zabývá pouze konzistencí vysílání, což je vlastnost, kdy jedna komponenta vysílá jednu hodnotu všem ostatním komponentám, všechny přijmou právě tuto hodnotu nebo v případě, že rozesílač není konzistentní, ostatní komponenty se dohodnou na společné hodnotě samy. Tento druh odolnosti proti selhání nezahrnuje korektnost samotné hodnoty; například nepřátelská komponenta, která úmyslně pošle nesprávnou hodnotu, ale pošle tuto hodnotu konzistentně všem komponentám, nebude ve schématu odolnosti proti byzantskému selhání zachycena.
Řešení
[editovat | editovat zdroj]Několik řešení popsali Lamport, Shostak, a Pease v roce 1982.[5] Povšimli si, že problém generálů lze redukovat na řešení problému „Velitele a poručíků“ kde všichni loajální poručíci musí fungovat ve shodě, a že jejich akce musí odpovídat tomu, co velitel nařídil, pokud je velitel je loajální:
- Jedno řešení uvažuje scénáře, ve kterým mohou být zprávy podvržené, ale které budou byzantsky odolné proti chybám, dokud podíl neloajálních generálů je menší než jedna třetina jejich počtu. Nemožnost vypořádat se s jednou třetinou nebo větším množstvím zrádců jednoznačně omezuje dokazování, že problém jednoho velitele a dvou poručíků nemůže být vyřešen, pokud velitel je zrádný. Abychom to viděli, předpokládejme, že máme zrádného velitele A, a dva poručíky B a C:, když A rozkazuje poručíkovi B zaútočit a poručíkovi C ustoupit, a B a C si navzájem posílají zprávy, pak ani B ani C nemůže zjistit, kdo je zrádce, protože to nemusí nutně být A; druhý poručík mohl zprávu od A zfalšovat. Lze ukázat, že pokud počet generálů je n a z nich je t zrádců, pak řešení problému existuje, pouze tehdy, když n > 3t a komunikace je synchronní (s omezeným zpožděním).[12]
- Druhé řešení vyžaduje nezfalšovatelné podpisy zpráv. Pro systémy kritické z hlediska bezpečnosti informací mohou digitální podpisy (v moderních počítačových systémech, jich lze v praxi dosáhnout použitím asymetrické kryptografie) poskytovat odolnost proti byzantskému selhání při existenci libovolného počtu zrádných generálů. Pro systémy kritické z hlediska bezpečnosti (kde „bezpečnost informací“ znamená odolnost proti inteligentním hrozbám, zatímco „bezpečnost“ je odolnost proti přirozeným nebezpečím činnosti nebo mise), jednoduché kódy pro detekci chyb, např. CRC, poskytují slabší, ale často postačující ochranu za mnohem nižší cenu. To platí pro byzantská i nebyzantská selhání. Někdy navíc bezpečnost informací oslabuje fyzickou bezpečnost a naopak. Metody kryptografického digitálního podpisu tedy nejsou dobrou volbou pro systémy vyžadující fyzickou bezpečnost, pokud neexistuje také konkrétní bezpečnostní hrozba.[13] Zatímco kódy pro detekci chyb, např. CRCs, jsou lepší než kryptografické techniky, ani jedno neposkytuje dostatečnou ochranu pro aktivní elektroniky v systémech kritických z hlediska fyzické bezpečnosti. To je ilustrováno scénářem Schrödingerova CRC, kde zpráva chráněná CRC s jediným byzantským vadným bitem prezentuje různá data různým pozorovatelům a každý pozorovatel zaznamená (vidí) platné CRC.[3][4]
- Také jsou prezentovány variace na první dvě řešení poskytující v některých situacích odolnost proti byzantským selháním, kde ne všichni generálové mohou vzájemně přímo komunikovat.
Kolem roku 1980 bylo navrženo několik architektur systému, které implementovaly odolnost proti byzantským selháním. Patří k nim: Draperovo FTMP,[14] MMFCS společnosti Honeywell,[15] a SIFT organizace SRI.[7]
V roce 1999 Miguel Castro a Barbara Liskovová představili algoritmus „Practical Byzantine Fault Tolerance“ (PBFT),[16] který poskytuje replikaci vysoce výkonných byzantských stavových strojů, zpracování tisíc požadavků za sekundu se submilisekundovým zvyšuje latence.
Po PBFT bylo navrženo několik BFT protokolů pro zlepšení jeho robustnosti a výkonnosti. Například Q/U,[17] HQ,[18] Zyzzyva,[19] a ABsTRACTs,[20] které jsou zaměřeny na otázky výkonnosti a ceny; naproti tomu jiné protokoly, jako Aardvark[21] a RBFT,[22] se zaměřovaly na problémy jeho robustnosti. Adapt[23] se pokoušel využít existující BFT protokoly a adaptivním přepojováním mezi nimi zlepšit robustnost a výkonnost systému při změnách podmínek. Byly také navrženy BFT protokoly, které vkládají důvěryhodné komponenty pro omezení počtu kopií, například A2M-PBFT-EA[24] a MinBFT.[25]
Příklady
[editovat | editovat zdroj]Několik příkladů byzantských selhání, ke kterým došlo, je uvedeno ve dvou ekvivalentních odborných článcích v časopisech.[3][4] Tyto a další příklady jsou popsány na WWW stránkách NASA DASHlink.[26]
Byzantské poruchy byly pozorovány nepříliš často a v nepravidelných intervalech během testování trvanlivosti nově zkonstruované třídy ponorek Virginia, přinejmenším do roku 2005 (kdy byly problémy veřejně oznámeny).[27]
Síť Bitcoin pracuje paralelně a vytváří blockchain s funkcí Proof-of-Work (důkaz vykonané práce), která umožňuje systému překonat byzantské chyby a dosáhnout koherentní globální pohledu na stav systému. Některé Proof-of-Stake blockchainy také používají BFT algoritmy.[28]
Některé letecké systémy, např. systém kontroly letu (Aircraft Information Management System využívající síť ARINC 659 SAFEbus) Boeingu 777 nebo 787 jsou založeny na odolnosti proti byzantskému selhání; protože jde o systémy pracující v reálném čase, jejich odolnost proti byzantskému selhání musí mít velmi nízké latence. Například SAFEbus může dosáhnout odolnosti proti byzantskému selhání v řádu mikrosekund dodatečné latence.[29][30][31] Projekt kosmické lodi Dragon se ve svém návrhu zabývá odolností proti byzantským poruchám.[32]
Mechanismy tolerance proti byzantským poruchám využívají komponenty, které opakují přicházející zprávy (nebo pouze jejich podpisy) jiným příjemcům této přicházející zprávy. Všechny tyto mechanismy předpokládají, že funguje opakování bloků zpráv šíření byzantských symptomů. Pro systémy, které mají vysoký stupeň bezpečnosti nebo jejichž bezpečnost je kritická, musí být prověřeno, že tyto předpoklady skutečně na přijatelné úrovni chrání před selháním. Při dokazování pomocí testování je jednou z potíží vytváření dostatečně širokého rozsahu signálů s byzantskými symptomy.[33] Takové testování pravděpodobně bude vyžadovat specializované injektory selhání.[34][35]
Odkazy
[editovat | editovat zdroj]Reference
[editovat | editovat zdroj]V tomto článku byl použit překlad textu z článku Byzantine fault na anglické Wikipedii.
- ↑ KIRRMANN, Hubert. Fault Tolerant Computing in Industrial Automation [online]. Switzerland: ABB Research Center, n.d. [cit. 2015-03-02]. S. 94. Dostupné v archivu pořízeném dne 2014-03-26.
- ↑ LAMPORT, L.; SHOSTAK, R.; PEASE, M., 1982. The Byzantine Generals Problem. ACM Transactions on Programming Languages and Systems. Roč. 4, čís. 3, s. 382–401. Dostupné v archivu pořízeném z originálu dne 2018-06-13. DOI 10.1145/357172.357176. S2CID 55899582.
- ↑ a b c d DRISCOLL, K.; HALL, B.; PAULITSCH, M.; ZUMSTEG, P.; SIVENCRONA, H., 2004. The 23rd Digital Avionics Systems Conference (IEEE Cat. No.04CH37576). [s.l.]: [s.n.]. ISBN 978-0-7803-8539-9. DOI 10.1109/DASC.2004.1390734. S2CID 15549497. Kapitola The Real Byzantine Generals, s. 6.D.4–61–11.
- ↑ a b c DRISCOLL, Kevin; HALL, Brendan; SIVENCRONA, Håkan; ZUMSTEG, Phil, 2003. Computer Safety, Reliability, and Security. [s.l.]: [s.n.]. (Lecture Notes in Computer Science). Dostupné online. ISBN 978-3-540-20126-7. DOI 10.1007/978-3-540-39878-3_19. S2CID 12690337. Kapitola Byzantine Fault Tolerance, from Theory to Reality, s. 235–248.
- ↑ a b c LAMPORT, L.; SHOSTAK, R.; PEASE, M., 1982. The Byzantine Generals Problem. ACM Transactions on Programming Languages and Systems. Roč. 4, čís. 3, s. 387–389. Dostupné v archivu pořízeném z originálu dne 2017-02-07. DOI 10.1145/357172.357176. S2CID 55899582.
- ↑ Matthias Fitzi, 2002. Generalized Communication and Security Models in Byzantine Agreement [online]. ETH Zurich, 2002. Dostupné online.
- ↑ a b , 1979. SIFT: design and analysis of a fault-tolerant computer for aircraft control. Microelectronics Reliability. Roč. 19, čís. 3, s. 190. ISSN 0026-2714. DOI 10.1016/0026-2714(79)90211-7.
- ↑ PEASE, Marshall; SHOSTAK, Robert; LAMPORT, Leslie. Reaching Agreement in the Presence of Faults. Journal of the Association for Computing Machinery. April 1980, roč. 27, čís. 2, s. 228–234. DOI 10.1145/322186.322188. S2CID 6429068.
- ↑ LAMPORT, Leslie. The Byzantine Generals Problem. ACM Transactions on Programming Languages and Systems. SRI International, 2016-12-19. Dostupné online [cit. 2019-03-18].
- ↑ AVIZIENIS, A.; LAPRIE, J.-C.; RANDELL, Brian; LANDWEHR, C., 2004. Basic concepts and taxonomy of dependable and secure computing. IEEE Transactions on Dependable and Secure Computing. Roč. 1, čís. 1, s. 11–33. ISSN 1545-5971. DOI 10.1109/TDSC.2004.2. S2CID 215753451.
- ↑ Dependable Computing and Fault Tolerance [online]. [cit. 2015-03-02]. Dostupné v archivu pořízeném z originálu dne 2015-04-02.
- ↑ FELDMAN, P.; MICALI, S., 1997. An optimal probabilistic protocol for synchronous Byzantine agreement. SIAM J. Comput.. Roč. 26, čís. 4, s. 873–933. Dostupné v archivu pořízeném z originálu dne 2016-03-05. DOI 10.1137/s0097539790187084.
- ↑ PAULITSCH, M.; MORRIS, J.; HALL, B.; DRISCOLL, K.; LATRONICO, E.; KOOPMAN, P., 2005. 2005 International Conference on Dependable Systems and Networks (DSN'05). [s.l.]: [s.n.]. Dostupné online. ISBN 978-0-7695-2282-1. DOI 10.1109/DSN.2005.31. S2CID 14096385. Kapitola Coverage and the Use of Cyclic Redundancy Codes in Ultra-Dependable Systems, s. 346–355.
- ↑ HOPKINS, Albert L.; LALA, Jaynarayan H.; SMITH, T. Basil, 1987. The Evolution of Fault-Tolerant Computing. [s.l.]: [s.n.]. (Dependable Computing and Fault-Tolerant Systems). ISBN 978-3-7091-8873-6. DOI 10.1007/978-3-7091-8871-2_6. Kapitola The Evolution of Fault Tolerant Computing at the Charles Stark Draper Laboratory, 1955–85, s. 121–140.
- ↑ DRISCOLL, Kevin; PAPADOPOULOS, Gregory; NELSON, Scott; HARTMANN, Gary; RAMOHALLI, Gautham, 1984. Multi-Microprocessor Flight Control System. Wright-Patterson Air Force Base, OH: AFWAL/FIGL U.S. Air Force Systems Command. AFWAL-TR-84-3076.
- ↑ CASTRO, M.; LISKOV, B., 2002. Practical Byzantine Fault Tolerance and Proactive Recovery. ACM Transactions on Computer Systems. Association for Computing Machinery. Roč. 20, čís. 4, s. 398–461. Dostupné online. DOI 10.1145/571637.571640. S2CID 18793794.
- ↑ ABD-EL-MALEK, M.; GANGER, G.; GOODSON, G.; REITER, M.; WYLIE, J., 2005. Fault-scalable Byzantine Fault-Tolerant Services. ACM SIGOPS Operating Systems Review. Association for Computing Machinery. Roč. 39, čís. 5, s. 59. DOI 10.1145/1095809.1095817.
- ↑ COWLING, James; MYERS, Daniel; LISKOV, Barbara, 2006. HQ Replication: A Hybrid Quorum Protocol for Byzantine Fault Tolerance. In: Proceedings of the 7thUSENIXSymposium on Operating Systems Design and Implementation. [s.l.]: [s.n.]. Dostupné online. ISBN 1-931971-47-1. S. 177–190.
- ↑ KOTLA, Ramakrishna; ALVISI, Lorenzo; DAHLIN, Mike; CLEMENT, Allen; WONG, Edmund. Zyzzyva: Speculative Byzantine Fault Tolerance. ACM Transactions on Computer Systems. Association for Computing Machinery, December 2009, roč. 27, čís. 4, s. 1–39. DOI 10.1145/1658357.1658358.
- ↑ GUERRAOUI, Rachid; KNEŽEVIC, Nikola; VUKOLIC, Marko, 2010. The Next 700 BFT Protocols. In: Proceedings of the 5th European conference on Computer systems. [s.l.]: EuroSys. Dostupné v archivu pořízeném z originálu dne 2011-10-02.
- ↑ CLEMENT, A.; WONG, E.; ALVISI, L. Making Byzantine Fault Tolerant Systems Tolerate Byzantine Faults. In: Symposium on Networked Systems Design and Implementation. [s.l.]: USENIX, April 22–24, 2009. Dostupné v archivu pořízeném z originálu dne 2010-12-25.
- ↑ AUBLIN, P.-L.; BEN MOKHTAR, S.; QUÉMA, V. RBFT: Redundant Byzantine Fault Tolerance. In: 33rd IEEE International Conference on Distributed Computing Systems. [s.l.]: International Conference on Distributed Computing Systems, 8.–11. července 2013. Dostupné v archivu pořízeném dne 2013-08-05.
- ↑ BAHSOUN, J. P.; GUERRAOUI, R.; SHOKER, A. 2015 IEEE International Parallel and Distributed Processing Symposium. [s.l.]: [s.n.], 2015-05-01. ISBN 978-1-4799-8649-1. DOI 10.1109/IPDPS.2015.21. S2CID 16310807. Kapitola Making BFT Protocols Really Adaptive, s. 904–913.
- ↑ CHUN, Byung-Gon; MANIATIS, Petros; SHENKER, Scott; KUBIATOWICZ, John. Proceedings of twenty-first ACM SIGOPS symposium on Operating systems principles. New York, NY, USA: ACM, 2007-01-01. (SOSP '07). ISBN 9781595935915. DOI 10.1145/1294261.1294280. S2CID 6685352. Kapitola Attested append-only memory, s. 189–204.
- ↑ VERONESE, G. S.; CORREIA, M.; BESSANI, A. N.; LUNG, L. C.; VERISSIMO, P. Efficient Byzantine Fault-Tolerance. IEEE Transactions on Computers. 2013-01-01, roč. 62, čís. 1, s. 16–30. ISSN 0018-9340. DOI 10.1109/TC.2011.221. S2CID 8157723.
- ↑ DRISCOLL, Kevin. Real System Failures [online]. NASA, 2012-12-11 [cit. 2015-03-02]. (DASHlink). Dostupné v archivu pořízeném z originálu dne 2015-04-02.
- ↑ WALTER, C.; ELLIS, P.; LAVALLEY, B., 2005. Ninth IEEE International Symposium on High-Assurance Systems Engineering (HASE'05). [s.l.]: [s.n.]. ISBN 978-0-7695-2377-4. DOI 10.1109/HASE.2005.23. S2CID 21468069. Kapitola The Reliable Platform Service: A Property-Based Fault Tolerant Service Architecture, s. 34–43.
- ↑ Deirmentzoglou, Papakyriakopoulos a Patsakis 2019, s. 28716.
- ↑ M., Paulitsch; DRISCOLL, K. Industrial Communication Technology Handbook, Second Edition. [s.l.]: CRC Press, 2015-01-09. ISBN 978-1-4822-0733-0. Kapitola Chapter 48:SAFEbus, s. 48–1–48–26.
- ↑ Thomas A. Henzinger; Christoph M. Kirsch. Embedded Software: First International Workshop, EMSOFT 2001, Tahoe City, CA, USA, October 8-10, 2001. Proceedings. [s.l.]: Springer Science & Business Media, 2001-09-26. Dostupné v archivu pořízeném z originálu dne 2015-09-22. ISBN 978-3-540-42673-8. S. 307–.
- ↑ YEH, Y.C., 2001. 20th DASC. 20th Digital Avionics Systems Conference (Cat. No.01CH37219). [s.l.]: [s.n.]. ISBN 978-0-7803-7034-0. DOI 10.1109/DASC.2001.963311. S2CID 61489128. Kapitola Safety critical avionics for the 777 primary flight controls system, s. 1C2/1–1C2/11.
- ↑ ELC: SpaceX lessons learned [LWN.net] [online]. [cit. 2016-07-21]. Dostupné v archivu pořízeném z originálu dne 2016-08-05.
- ↑ NANYA, T.; GOOSEN, H.A., 1989. The Byzantine hardware fault model. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. Roč. 8, čís. 11, s. 1226–1231. ISSN 0278-0070. DOI 10.1109/43.41508.
- ↑ MARTINS, Rolando; GANDHI, Rajeev; NARASIMHAN, Priya; PERTET, Soila; CASIMIRO, António; KREUTZ, Diego; VERÍSSIMO, Paulo, 2013. Middleware 2013. [s.l.]: [s.n.]. (Lecture Notes in Computer Science). ISBN 978-3-642-45064-8. DOI 10.1007/978-3-642-45065-5_3. S2CID 31337539. Kapitola Experiences with Fault-Injection in a Byzantine Fault-Tolerant Protocol, s. 41–61.
- ↑ Method for testing the sensitive input range of Byzantine filters. Původce vynálezu: KEVIN R. DRISCOLL. Patent. US. Patentový spis 7475318. 2006-01-27.
Literatura
[editovat | editovat zdroj]- DEIRMENTZOGLOU, Evangelos; PAPAKYRIAKOPOULOS, Georgios; PATSAKIS, Constantinos, 2019. A Survey on Long-Range Attacks for Proof of Stake Protocols. IEEE Access. Roč. 7, s. 28712–28725. DOI 10.1109/ACCESS.2019.2901858. S2CID 84185792.
Související články
[editovat | editovat zdroj]- Atomický commit
- Brooksův–Iyengarův algoritmus
- Paxos (informatika)
- Kvantová byzantská dohoda
- Problém dvou armád
- Bezkonfliktní replikovaný datový typ
Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu Problém byzantských generálů na Wikimedia Commons
Obrázky, zvuky či videa k tématu Problém byzantských generálů na Wikimedia Commons - odolnost Byzantine Fault Tolerance in the RKBExplorer
