Lemma devíti
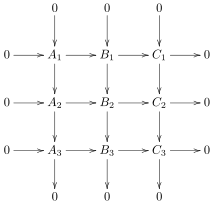
Lemma devíti (nebo lemma 3×3) je v matematice tvrzení o komutativních diagramech a exaktních posloupnostech platné v kategorii grup Grp a v libovolné Abelově kategorii. Říká: pokud diagram vpravo komutuje a všechny sloupce i dva spodní řádky jsou exaktní, pak horní řádek je také exaktní. Podobně pokud jsou všechny sloupce a dva horní řádky exaktní, pak spodní řádek je také exaktní. Navíc, protože diagram je symetrický podle své diagonály, platí stejné tvrzení, když vzájemně prohodíme řádky a sloupce.
Lemma devíti lze dokázat jednoduchým procházením diagramu nebo použitím hadího lemmatu (v prvním případě na dva spodní řádky, ve druhém na dva horní řádky).
Linderholm nabízí satirický pohled na lemma devíti:
Nakreslete hrací pole pro piškvorky… Nevyplňujte jej kolečky a křížky… Místo toho, použijte zakřivené šipky… Mávejte nad touto tabulí rukama ve složitých vzorcích. Udělejte nějaká kolečka, ale ne ve čtvercích; dejte je na oba konce horizontálních i vertikálních přímek. Udělejte pár ksichtů. Tím jste dokázali:
(a) Lemma devíti
(b) Lemma šestnácti
(c) Lemma dvaceti pěti…[1]
Existují dvě varianty lemmatu devíti: ostré lemma devíti a symetrické lemma devíti (viz Lemma 3.3 a 3.4 v Chapter XII v Saundersově knize o homologii.[2])
Odkazy
[editovat | editovat zdroj]Reference
[editovat | editovat zdroj]V tomto článku byl použit překlad textu z článku Nine lemma na anglické Wikipedii.
- ↑ Linderholm 1971, s. 201.
- ↑ MACLANE, Saunders, 1967. Homology. Berlin [u.a.]: Springer. ISBN 9783540586623. S. 365–366.
- LINDERHOLM, Carl, 1971. Mathematics Made Difficult. [s.l.]: Wolfe. Dostupné online. ISBN 0-7234-0415-1.
