Fibonacciho halda

Fibonacciho halda je druh haldy. Principiálně vychází z binomiální haldy. Hlavní výhodou Fibonacciho haldy je nízká asymptotická složitost prováděných algoritmů. Operace vložení, hledání minima, snížení hodnoty klíče a spojování stromů probíhají v konstantním čase, amortizovaně O(1). Operace mazání a mazání minimálního prvku pracuje s časovou složitostí O(log n), přičemž k výraznému zrychlení výpočtů oproti binomiální haldě dochází zejména v momentě, kdy některá z větví stromu neobsahuje žádná data.

Mezi nejčastější aplikace Fibonacciho haldy patří Jarníkův a Dijkstrův algoritmus, které slouží k vyhledávání minimální kostry grafu a k určení nejkratší cesty v grafu.

Pojem Fibonacciho haldy zavedli Michael L. Fredman a Robert E. Tarjan v roce 1984 a poprvé jej publikovali v roce 1987 ve vědeckých časopisech. Označení Fibonacciho halda vychází z Fibonacciho čísel, která mají souvislost s počtem vrcholů v každém stromě.

Obrázek 1: Počty vrcholů stromů F0, F1, … tvoří Fibonacciho posloupnost

Struktura Fibonacciho haldy

Obrázek 2: Příklad Fibonacciho haldy, která je tvořena třemi stromy stupňů 0, 1 a 3. Tři prvky jsou zvýrazněny (modrou barvou). Potence haldy je 9.

Fibonacciho haldu tvoří skupina stromů vyhovující lokální podmínce na uspořádání haldy (tzv. vlastnosti haldy), která vyžaduje, aby pro každý uzel stromu platilo, že prvek, který reprezentuje, je menší než prvek reprezentovaný jeho potomky. Z této podmínky vyplývá, že minimálním prvkem je vždy kořen jednoho ze stromů. Vnitřní struktura Fibonacciho haldy je v porovnání s binomiální haldou daleko více flexibilní. Jednotlivé stromy nemají pevně daný tvar a v extrémním případě může každý prvek haldy tvořit izolovaný strom nebo naopak všechny prvky mohou být součástí jediného stromu hloubky N. Tato flexibilní struktura umožňuje velmi jednoduchou implementaci operací s haldou. Operace, které nejsou potřebné, odkládáme a vykonáváme je až v okamžiku, kdy je to nevyhnutelné, například spojení nebo vložení nového prvku se jednoduše provede spojením kořenových seznamů (s konstantní náročností) a jednotlivé stromy spojíme až při operaci snížení hodnoty klíče.

Obecně lze říci, že stupeň uzlu (zde je stupeň myšlen jako počet synů prvku) je velmi nízký: každý uzel má stupeň nejvýše log N a velikost podstromu vycházejícího z uzlu stupně K je nejméně F_K+2, kde F_K je K-té Fibonacciho číslo. Toho je dosaženo díky pravidlu, které dovoluje oříznout nejvýše jednoho syna od každého nekořenového prvku. Pokud je odříznut druhý syn, uzel musí být odříznut od svého otce a stává se kořenem nového stromu. Počet stromů je snižován při operaci odstranění prvku s nejnižší hodnotou klíče, kdy dochází ke spojování stromů.

Implementace operací (algoritmů)

Pro rychlé vymazání a zřetězení se vytváří obousměrný cyklický spojový seznam kořenů všech stromů. Pro potomky každého prvku se vytváří podobný seznam. Pro každý uzel se ukládá počet synů a údaj, zda je zvýrazněn. Navíc si uchováváme ukazatel na kořenový prvek s minimální hodnotou klíče.

Mezi základní operace patří vytvoření prázdné haldy, hledání minimálního prvku, odstranění minimálního prvku, vložení nového prvku do haldy, snížení hodnoty klíče daného prvku, zřetězení dvojice hald, slévání stromů a další. Některé z nich si popíšeme podrobněji.

Hledání minimálního prvku

Operace hledání minima je velmi triviální, protože máme vytvořený ukazatel na příslušný uzel. Tato operace nemění potenci haldy, a její složitost nabývá konstantních hodnot O(1).

Zřetězení dvojice hald

Jak bylo zmíněno výše, zřetězení se provádí prostým spojením seznamů s kořenovými prvky stromů jednotlivých hald. Operace je provedena s konstantní amortizovanou složitostí a bez změny potence.

Slévání stromů

Při slévání stromů tvořících jednu haldu postupně sjednotíme kořeny stromů stejných stupňů. Uvažujeme, že počet kořenových prvků na počátku operace je N. Pokud máme dva kořeny U a V stejného stupně, vytvoříme z jednoho z nich syna druhého prvku tak, aby kořenovým zůstal prvek s menší hodnotou klíče. Jeho stupeň se pak zvětší o jedničku. Toto opakujeme, dokud v haldě existují dva stromy se stejným stupněm. K efektivnímu hledání stromů stejného stupně používáme pole ukazatelů, ve kterém uchováváme reference vždy na jeden kořen každého stupně. Pokud je nalezen druhý strom stejného stupně, oba stromy jsou spojeny a příslušný ukazatel v poli je aktualizován. Amortizovaná složitost tohoto algoritmu je O(log N).

Odstranění minimálního prvku

Fibonacciho halda z obrázku 2 po prvním kroku odstranění minimálního prvku. Uzel s hodnotou klíče 1 (minimum) je odstraněn a z jeho synů jsou vytvořeny samostatné stromy.

Fibonacciho halda z obrázku 2 po provedení operace odstranění minimálního prvku. Nové minimum je prvek 2.

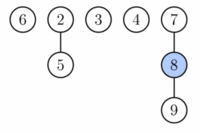
Operace odstranění minima probíhá ve třech krocích. V prvním odstraníme kořenový prvek s minimální hodnotou klíče. Jeho synové vytvoří kořenové prvky nových stromů. Počet těchto synů označíme D. Amortizovaná složitost tohoto kroku je pak O(D) = O(log N).

Jakmile je starý minimální prvek z haldy odstraněn, musíme najít nový kořenový prvek s minimální hodnotou klíče. Nevýhodou je vysoký počet kořenových prvků, jež může dosahovat hodnoty až N. V druhém kroku proto snížíme počet kořenových prvků tak, že provedeme slévání stromů.

Ve třetím kroku procházíme všechny zbývající kořenové prvky a z nich hledáme nové minimum. Potence haldy se při tomto kroku nemění.

Vložení nového prvku do haldy

Při operaci vložení nového prvku dojde k vytvoření nové haldy a následně k jejímu zřetězení s haldou původní. Operace opět proběhne s konstantní amortizovanou složitostí, pouze potence haldy vzroste o jednu.

Snížení hodnoty klíče daného prvku

Fibonacciho halda z obrázku 2 po provedení operace snížení hodnoty klíče prvku 9 na 0. Tento prvek je, právě tak jako dva označení otcové, odříznut od stromu s kořenem 1 a umístěný jako nový strom.

Operace snížení hodnoty klíče prvku změní hodnotu klíče na zadanou a současně provede kontrolu, zda je splněna lokální podmínka uspořádání haldy (tedy hodnota klíče otce je menší než hodnota klíče jeho syna). V případě, kdy tato podmínka není splněna, dojde k odříznutí prvku od jeho otce a přidání jako nového stromu. Pokud otec není kořenovým prvkem, je zvýrazněn. Pokud již zvýrazněn byl, bude také odříznut a přidán jako nový strom a jeho otec zvýrazněn. Stejným způsobem proces pokračuje vzhůru, dokud nedosáhne kořenového prvku nebo neoznačeného vrcholu. Počet stromů, které nově vzniknou při tomto procesu, si označíme jako K. Ze všech prvků, které byly zvýrazněné a staly se kořenovými prvky nových stromů, se zvýraznění odstraní. Naopak jeden prvek mohl být nově zvýrazněn. Potence byla snížena minimálně o K – 2. Operační náročnost snížení hodnoty klíče je konstantní, amortizovaně O(K).

Odstranění obecného prvku

Operace odstranění obecného prvku se skládá ze dvou kroků. Nejprve se provede snížení hodnoty klíče tohoto prvku tak, aby se tento prvek stal minimálním v celé haldě (např. snížení na hodnotu -∞, nebo při programování na minimální hodnotu příslušného datového typu). Druhým krokem je odstranění minimálního prvku. Amortizovaná složitost tohoto kroku je O(log n).

Použití Fibonacciho haldy

Přestože operační náročnost algoritmů prováděných s Fibonacciho haldou je nízká, může nastat situace, kdy operace startující s prázdnou strukturou mohou být výrazně časově náročné (zvláště snížení hodnoty klíče, odstranění prvku s minimální hodnotou klíče může v nejhorším případě nabývat lineární časové závislosti). Z tohoto důvodu nejsou Fibonacciho haldy a jiné amortizované datové struktury vhodné pro systémy běžící v reálném čase.

Reference

V tomto článku byl použit překlad textu z článku Fibonacci heap na anglické Wikipedii.

• Fredman M. L. & Tarjan R. E. (1987). Fibonacci heaps and their uses in improved network optimization algorithms. Journal of the ACM 34(3), 596-615.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 20: Fibonacci Heaps, pp.476–497.

Související články

• Dijkstrův algoritmus
• Jarníkův algoritmus

Externí odkazy

• Vizualizace binomiální haldy, lenivé binomiální haldy a Fibonacciho haldy
• Implementace Fibonacci haldy v jazyce C