Z Wikipedie, otevřené encyklopedie
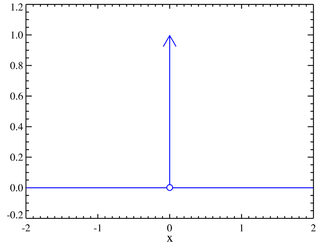
Schematická reprezentace Diracovy
δ
{\displaystyle \delta }
Diracova funkce jako limita
δ
(
x
)
=
lim
a
→
0
+
1
a
π
e
−
x
2
/
a
2
{\displaystyle \delta (x)=\lim _{a\to 0^{+}}{\frac {1}{a{\sqrt {\pi }}}}e^{-x^{2}/a^{2}}}
Diracovo delta nebo Diracova
δ
{\displaystyle \delta }
se dá neformálně popsat jako funkce, která má v nule hodnotu nekonečno a všude jinde nulovou. Je značena řeckým písmenem delta . Její integrál přes celý prostor je roven jedné.
δ
(
x
)
=
{
+
∞
pro
x
=
0
0
pro
x
≠
0
{\displaystyle \delta (x)=\left\{{\begin{matrix}+\infty &{\mbox{pro }}x=0\\0&{\mbox{pro }}x\neq 0\end{matrix}}\right.}
∫
−
∞
∞
δ
(
x
)
d
x
=
1
{\displaystyle \int _{-\infty }^{\infty }\delta (x)\,\mathrm {d} x=1}
∫
−
∞
x
δ
(
t
)
d
t
=
H
(
x
)
{\displaystyle \int _{-\infty }^{x}\delta (t)\,\mathrm {d} t=H(x)}
Heavisideovu funkci V souvislosti se zpracováním signálu bývá Diracova funkce označována také jako Diracův jednotkový impuls . (Jednotkový právě pro integrál rovný jedné)
V exaktním matematickém popisu není Diracova delta funkcí , ale distribucí . Diskrétním ekvivalentem Diracova delta je Kroneckerovo delta .
Diracovu
δ
{\displaystyle \delta }
komplexní čísla například ve tvaru integrálu .
δ
(
x
)
=
1
2
π
∫
−
∞
∞
e
i
k
x
d
k
{\displaystyle \delta (x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\mathrm {e} ^{ikx}\,\mathrm {d} k}
[ 1] Nebo pomocí limit .
δ
(
x
)
=
lim
L
→
∞
sin
x
L
x
π
{\displaystyle \delta (x)=\lim _{L\to \infty }{\frac {\sin xL}{x\pi }}}
[ 2]
δ
(
x
)
=
lim
a
→
0
+
1
π
a
a
2
+
x
2
{\displaystyle \delta (x)=\lim _{a\to 0^{+}}{\frac {1}{\pi }}{\frac {a}{a^{2}+x^{2}}}}
[ 3]
δ
(
x
)
=
lim
a
→
0
+
1
a
π
e
−
x
2
/
a
2
{\displaystyle \delta (x)=\lim _{a\to 0^{+}}{\frac {1}{a{\sqrt {\pi }}}}\mathrm {e} ^{-x^{2}/a^{2}}}
[ 4] Označení posunuté („doprava“) delta funkce:
δ
a
(
x
)
≡
δ
(
x
−
a
)
{\displaystyle \delta _{a}(x)\equiv \delta (x-a)}
Delta funkce je sudá funkce.
δ
(
x
)
=
δ
(
−
x
)
{\displaystyle \delta (x)=\delta (-x)}
Působí jako jednotkový operátor při integraci.
∫
−
∞
∞
f
(
x
)
δ
(
x
−
a
)
d
x
=
∫
−
∞
∞
f
(
x
)
δ
a
(
x
)
d
x
=
f
(
a
)
{\displaystyle \int _{-\infty }^{\infty }f(x)\delta (x-a)\,\mathrm {d} x=\int _{-\infty }^{\infty }f(x)\delta _{a}(x)\,\mathrm {d} x=f(a)}
Konvoluce libovolné funkce s delta funkcí je rovna této funkci.
f
(
x
)
∗
δ
(
x
)
=
δ
(
x
)
∗
f
(
x
)
=
f
(
x
)
{\displaystyle f(x)*\delta (x)=\delta (x)*f(x)=f(x)}
Konvoluce s posunutou delta funkcí má za následek posunutí této funkce.
f
(
x
)
∗
δ
a
(
x
)
=
f
(
x
−
a
)
{\displaystyle f(x)*\delta _{a}(x)=f(x-a)}
F
[
δ
(
x
)
]
=
D
(
ξ
)
=
1
{\displaystyle {\mathcal {F}}\left[\delta (x)\right]=D(\xi )=1}
Z toho plyne, že zpětná Fourierova transformace jednotkové funkce je ve smyslu distribuce rovna delta funkci.
δ
(
x
)
=
∫
−
∞
∞
e
2
π
i
x
ξ
d
ξ
{\displaystyle \delta (x)=\int _{-\infty }^{\infty }\mathrm {e} ^{\,2\pi ix\,\xi }\,\mathrm {d} \xi }
Pro Fourierovu transformaci posunuté delta funkce platí:
F
[
δ
a
(
x
)
]
=
D
a
(
ξ
)
=
e
−
2
π
i
a
ξ
{\displaystyle {\mathcal {F}}\left[\delta _{a}(x)\right]=D_{a}(\xi )=\mathrm {e} ^{-2\pi ia\,\xi }}
Je-li
f
(
x
)
{\displaystyle f(x)}
f
(
x
i
)
=
0
{\displaystyle f(x_{i})=0}
δ
(
f
(
x
)
)
=
∑
i
δ
(
x
−
x
i
)
|
f
′
(
x
i
)
|
{\displaystyle \delta (f(x))=\sum _{i}{\frac {\delta (x-x_{i})}{|f'(x_{i})|}}}
x
δ
(
x
)
=
0
{\displaystyle x\delta (x)=0\,}
δ
(
a
x
)
=
δ
(
x
)
|
a
|
{\displaystyle \delta (ax)={\frac {\delta (x)}{|a|}}\,}
f
(
x
)
δ
(
x
−
a
)
=
f
(
a
)
δ
(
x
−
a
)
{\displaystyle f(x)\delta (x-a)=f(a)\delta (x-a)\,}
∫
−
∞
∞
δ
(
a
−
x
)
δ
(
x
−
b
)
d
x
=
δ
(
a
−
b
)
{\displaystyle \int _{-\infty }^{\infty }\delta (a-x)\delta (x-b)\,\mathrm {d} x=\delta (a-b)\,}
δ
(
x
2
−
a
2
)
=
δ
(
x
−
a
)
+
δ
(
x
+
a
)
2
|
a
|
{\displaystyle \delta (x^{2}-a^{2})={\frac {\delta (x-a)+\delta (x+a)}{2|a|}}\,}
![{\displaystyle {\mathcal {F}}\left[\delta (x)\right]=D(\xi )=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b9c62a205e0d12c3070f3109ad89f1d3bc17339)
![{\displaystyle {\mathcal {F}}\left[\delta _{a}(x)\right]=D_{a}(\xi )=\mathrm {e} ^{-2\pi ia\,\xi }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a2e7b574391a0d2632e83182a50a55814ac93c0)
Obrázky, zvuky či videa k tématu Diracovo delta na Wikimedia Commons 