Zakódovaný obrázek

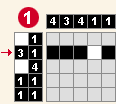
Zakódovaný obrázek (nonogram, kódovaný obrázek či malovaná křížovka) je logický hlavolam, při kterém je okolo mřížky umístěná legenda s čísly a pomocí nich lze získat obrázek. Každé číslo v legendě určuje počet za sebou následujících čtverečků stejné barvy.
V Česku se zakódované obrázky objevují od první půlky 90. let v časopise Panorama křížovek, kde byly otiskovány i nejednoznačně zadané obrázky vyžadující hádání. V dalším desetiletí se objevují specializované tituly, vycházející v periodě čtvrtletní, dvouměsíční i měsíční. Vyšlo i několik jednorázových knižních publikací. V české distribuční síti převažují tituly původem ze Slovenska (odkud pochází označení Malované křížovky) a jejich distribuce probíhá pouze přes některé prodejce tisku.
Princip zakódovaných obrázků
[editovat | editovat zdroj]Postup krok za krokem
[editovat | editovat zdroj]
Seznam typů zakódovaných obrázků
[editovat | editovat zdroj]- Klasické (Nonogram, Griddler) – čtvercová mřížka s černobílým obrázkem
- Trojúhelníkové – na rozdíl od klasického zakódovaného obrázku obsahují 4 typy diagonálně rozpůlených polí, které zlepšují rozpoznání obrázku
- mezi číslem a trojúhelníkem nemusí být mezera
- Barevné – barva buněk je zadána barvou číselného zadání, možné je i nebílé pozadí zadané v levém horním rohu
- Multiobrázky – výsledný obrázek je složen z několika menších částí, které se luští zvlášť
- Triddler – trojúhelníková mřížka, číselné zadání se vyskytuje ze tří stran
- Bludiště – obrázek vznikne vybarvením cesty skrz bludiště
- Mozaika – každé číslo označuje počet vybarvených polí v nejbližším okolí (0–9), princip podobný hře Hledání min
- ParX (Link-a-Pix) – spojují se dvojice čísel (kromě čísla 1), spojnice tvoří obrázek
- Cross-a-Pix – mřížka je rozdělena do segmentů, které jsou buď plné nebo prázdné
- čísla na krajích uvádí počet vybarvených polí v daném sloupci nebo řádku bez ohledu na mezery
- číselné zadání může být doplněno počtem segmentů v daném sloupci nebo řádku
- Sym-a-Pix – mřížka je vyplněna body označujícími těžiště bodově symetrických obrazců, barva bodu určuje barvu obrazce
Zakódované obrázky v elektronické podobě
[editovat | editovat zdroj]Zakódované obrázky existují v digitální podobě na internetu od konce devadesátých let 20. století. Existuje několik webových stránek, kde se setkává komunita luštitelů a kromě luštění vytvářejí obrázky pro ostatní. Tyto stránky umožňují hodnotit obtížnost a krásu vyluštěného obrázku nebo porovnávat čas potřebný k řešení.
Zakódované obrázky existují v různých podobách i jako aplikace pro dotykové telefony a tablety. Při luštění zakódovaných obrázků je výhodné mít přehled o celé mřížce a vidět stále legendu, proto je pro luštění větších obrázků vhodnější tablet než mobilní telefon.
Zakódované obrázky v informatice
[editovat | editovat zdroj]Řešení zakódovaných obrázků je NP-úplný problém.[1] To znamená, že existence polynomiálního algoritmu řešícího malovanou křížovku implikuje P = NP. Přesto platí, že existují efektivní algoritmy pro řešení některých typů obrázků.[2]
Reference
[editovat | editovat zdroj]- ↑ UEDA, Nobuhisa; NAGAO, Tadaaki. NP-completeness results for NONOGRAM via Parsimonious Reductions. Technical Report, Department of Computer Science, Tokyo Institute of Technology: [s.n.], 1996.
- ↑ BRUNETTI, Sara; DAURAT, Alain. An algorithm reconstructing convex lattice sets. Theoretical Computer Science. 2003, s. 35–57. Dostupné online. DOI 10.1016/S0304-3975(03)00050-1.
Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu malovaná křížovka na Wikimedia Commons
Obrázky, zvuky či videa k tématu malovaná křížovka na Wikimedia Commons - www.gameLO.net – Online sbírka zakódovaných obrázků
- Conceptis puzzles – Mnoho různých typů zakódovaných obrázků
- Griddlers Solver – Freeware se silným algoritmem řešení a animacemi řešení
- Picross-Time.net