Komplexní sloučenina
Komplexní sloučenina (nebo také koordinační sloučenina) je chemická sloučenina, která obsahuje alespoň jednu koordinačně-kovalentní vazbu. Často se jedná o sloučeniny přechodných kovů s Lewisovými bázemi. Obor chemie, který se zabývá těmito sloučeninami, se nazývá koordinační chemie.
Druhy kovových komplexů
[editovat | editovat zdroj]- Klasické komplexy (Wernerovy komplexy) – ligandy jsou vázány ke kovu pomocí volného elektronového páru. Mezi typické ligandy patří H2O, NH3, Cl−, atd. Jde např. o [Co(NH3)6]Cl3
- Organokovové komplexy – jako ligandy zde vystupují organické sloučeniny, například alkany, alkeny a fosfiny. Jde mimo jiné o ferrocen a další metaloceny.
- Bioanorganické komplexy – ligandy pocházejí z biologických systémů a obsahují například řetězce aminokyselin nebo porfyriny, patří sem mimo jiné hemoglobin.
- Klastry – tyto sloučeniny obsahují více atomů kovu, které jsou vázány přímou vazbou kov–kov. Jde například o Ru3(CO)12.
Koordinační číslo
[editovat | editovat zdroj]Pro určení struktury koordinační sloučeniny je důležitá znalost koordinačního čísla, což je počet vazeb σ mezi centrálním atomem a ligandy. Toto číslo odpovídá počtu ligandů pouze v případě jednovazných (monodentátních) ligandů. Hodnota koordinačního čísla běžných komplexů se pohybuje mezi dvěma a devíti, ale například u lanthanoidů lze pozorovat i vyšší koordinační čísla. Maximální koordinační číslo je dáno elektronovou konfigurací centrálního atomu, poměrem velikostí ligandu a centrálního atomu, vlivem náboje centrálního atomu a počtem volných vazebných orbitalů centrálního atomu.
Díky elektronovým efektům jako je Jahnův–Tellerův efekt jsou některá geometrická uspořádání stabilnější než jejich alternativy, například pro některé sloučeniny je trigonální prisma výhodnější než oktaedrická struktura.
Struktura základních koordinačních čísel je popsána níže, rozsáhlejší článek pojednávající o tomto tématu je koordinační číslo. Některé ligandy mají vžité zkratky, které se ve vzorcích používají, jejich význam je uveden na stránce o názvosloví koordinačních sloučenin.
Koordinační číslo 2
[editovat | editovat zdroj]Toto číslo je známo pouze u komplexů Cu+, Ag+, Au+ a Hg2+, které mají plně zaplněné d-orbitaly. Struktura těchto komplexů je lineární. Typickým příkladem je kation diamminostříbrný [Ag(NH3)2]+, který je znázorněn na obrázku.

Koordinační číslo 3
[editovat | editovat zdroj]Toto koordinační číslo je velmi vzácné. Je známé jen u některých komplexů s objemnými ligandy jako je například [Cu{SC(NH2)2}3]+. Z komplexů s jednoduššími ligandy je toto koordinační číslo známo pouze u trijodidortuťnatého aniontu [HgI3]− v kombinaci s vhodným kationtem (na obrázku). Tvar komplexu je rovnostranný trojúhelník. U některých komplexů je toto koordinační číslo pouze zdánlivé – například [CuCl3]− má ve skutečnosti polymerní koordinační číslo 4.
Koordinační číslo 4
[editovat | editovat zdroj]Toto koordinační číslo je druhé nejběžnější a odpovídá mu tetraedrické a čtvercové uspořádání koordinační sféry. Výběr mezi oběma geometriemi závisí do určité míry na elektronové konfiguraci centrálního atomu.
Jestliže jde o atom se sféricky symetrickou elektronovou konfigurací (elektrony jsou pravidelně uspořádány kolem jádra), pak se budou ligandy snažit uspořádat tak, aby byly co nejdále od sebe. Tomu odpovídá tetraedrické uspořádání. Tato situace nastává u komplexů s a p-prvků (např. [BF4]−) a u těch d-prvků, které buď dosáhly skupinového oxidačního čísla (všechny orbitaly prázdné, například Mn+7 – MnO4−), nebo mají konfiguraci d5 příp. d10 (symetrické konfigurace, např. Fe+3, Cu+ – [Cu(py)4]+, Ni0 – [Ni(CO)4]).
Centrální atomy s jinou konfigurací budou upřednostňovat čtvercové uspořádání komplexů. Platí to především pro konfiguraci d8 (Pd+2, Pt+2), která ve většině případů vede ke čtvercovému uspořádání (výjimku tvoří Ni2+, který tvoří běžně také tetraedrické komplexy). Čtvercové uspořádání ovšem vyžaduje alespoň jeden volný d orbital pro hybridizaci dsp2.
Jsou-li rozdíly v energii mezi čtvercovým a tetraedrickým uspořádáním malé (jako u některých komplexů Ni+2 nebo Cu+2), mohou existovat komplexy v obou geometriích nebo může mezi oběma docházet k vzájemné přeměně – (NH4)2[CuCl4] je čtvercový a Cs2[CuBr4] je přibližně tetraedrický. Čtverec a tetraedr jsou pak spíše extrémními možnostmi uspořádání ligandů a skutečný tvar leží někde mezi nimi. Tento jev se nazývá konformační izomerie a je o něm pojednáno níže.

Koordinační číslo 5
[editovat | editovat zdroj]Koordinační číslo 5 bylo dříve považováno za vzácné. Dnes jsou známy komplexy s tímto koordinačním číslem od všech centrálních atomů s konfigurací od d1 do d9. Tomuto koordinačnímu číslu odpovídají dvě mezní struktury – čtvercová pyramida ([VO(acac)3]) a trigonální bipyramida. Jelikož energie přeměny jedné limitní struktury v druhou je často malá, má většina komplexů strukturu odpovídající přechodu mezi oběma geometriemi. Mnohé sloučeniny s pětivazným centrálním atomem se chovají způsobem označovaným jako fluxionální, to znamená, že existují ve dvou nebo více chemicky ekvivalentních strukturách, které přecházejí jedna v druhou takovou rychlostí, že je nelze vzájemně rozlišit fyzikálním měřením.
Určitou výjimkou u tohoto koordinačního čísla jsou komplexy (především Ni+2 a Co+2) s „tripodovými“ ligandy, například P(CH2CH2PR2)3, které si svou strukturou vynucují jednoznačně tvar trigonální bipyramidy.

Koordinační číslo 6
[editovat | editovat zdroj]Toto koordinační číslo je nejběžnější a odpovídá mu oktaedrické a trigonálně prizmatické uspořádání koordinační sféry. Komplexy jsou výhradně oktaedrické. Právě na těchto komplexech Alfred Werner obhajoval svou teorii o koordinačních sloučeninách. Podařilo se připravit pouze několik trigonálně prizmatických komplexů – jako jsou [Re(S2C2Ph2)3].
V reálných komplexech je oktaedr vždy nějakým způsobem deformován. I pokud se jedná o komplex s homogenní koordinační sférou (například šest stejných ligandů), dochází k deformacím vlivem Jahnova–Tellerova efektu. Ten je způsoben nerovnoměrným rozložením elektronů centrálního atomu.
Existují v podstatě tři typy deformací pravidelného oktaedru: protažení nebo stlačení ve směru dvou protilehlých vrcholů, protažení nebo stlačení ve směru dvou protilehlých stěn a vzájemná rotace dvou protilehlých stěn. Poslední deformace vede v krajním případě až k tvaru trigonálního prizmatu.

Koordinační číslo 7
[editovat | editovat zdroj]Tomuto koordinačnímu číslu odpovídají tři základní prostorová uspořádání : pentagonální bipyramida ([ZrF7]3− a [HfF7]3−) a očepičkované trigonální prizma ([NbF7]2− a [TaF7]2−) a očepičkovaný oktaedr ([NbF6O]) (sedmý ligand je umístěn nad některou ze stěn trigonálního prizmatu a oktaedru).
Podobně jako u všech dalších vyšších koordinačních čísel je rozdíl energií mezi těmito uspořádáními velmi malý a o konkrétním tvaru rozhodují především sterické požadavky ligandů.

Koordinační číslo 8
[editovat | editovat zdroj]Nejpravidelnějším uspořádáním pro koordinační číslo 8 je krychle, přesto se tento tvar u komplexů prakticky nevyskytuje. Díky vzájemnému odpuzování ligandů dochází k deformacím, které vedou na tvar dodekaedru ([ZrF8]4− a [Mo(CN)8]4− nebo čtvercového antiprizmatu ([TaF8]3− a [ReF8]2−) (krychle s horní stěnou pootočenou o 45°). Rozdíl energií mezi těmito uspořádáními je velmi malý a o konkrétním tvaru rozhodují především sterické požadavky ligandů.

Koordinační číslo 9
[editovat | editovat zdroj]Většina komplexů s tímto koordinačním číslem má tvar trojbokého hranolu, kde nad každou ze tří svislých stěn je umístěn další ligand (na obrázku) ([ReH9]2−) (jde v podstatě o trigonální prizma, které má nad každou ze svých stěn ještě jeden ligand). Existují i jiná uspořádání, ale mnohá z nich jsou velmi nepravidelná.

Koordinační čísla větší než 9
[editovat | editovat zdroj]Tato koordinační čísla nejsou běžná a vyskytují se především u lehčích lanthanoidů a aktinoidů. Tedy u atomů s dostatečně velkým atomovým poloměrem. Navíc je nutné soudit, že k dosažení takto vysokých koordinačních čísel jsou nutné orbitaly f. Pro koordinační číslo 10 existuje komplex [La(H2O)4edta], pro koordinační číslo 11 [La(dapbah)(NO3)3], pro koordinační číslo 12 [Ce(NO3)6]3−. Vyšší koordinační čísla již nejsou ani mezi lanthanoidy a aktinoidy častá, ale vyskytují až do koordinačního čísla 16.
Izomerie koordinačních sloučenin
[editovat | editovat zdroj]U komplexních sloučenin je izomerie velmi častým jevem. Jsou to sloučeniny se stejným chemickým složením, ale rozdílnou strukturou. Můžeme rozlišit několik základních typů tohoto jevu:
Konformační izomerie přichází v úvahu pro každé koordinační číslo vyšší než 3 a jakoukoliv jemu odpovídající geometrii. Izomery se navzájem liší pouze svou stereochemií. Např. existuje [NiBr2(PEtPh2)2], který byl připraven jako zelený tetraedrický i jako žlutý čtvercový komplex. Konformační izomery musí mít srovnatelnou stabilitu a aby je bylo možné od sebe oddělit, musí existovat dostatečně vysoká energetická bariéra pro jejich vzájemnou přeměnu.
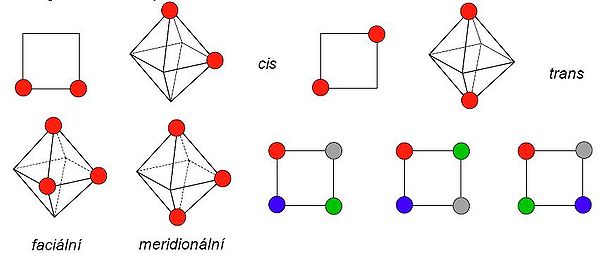
Geometrická izomerie vzniká u komplexů, jejichž koordinační číslo je větší než 3. S geometrickou izomerií se nejčastěji setkáváme u čtvercových a oktaedrických komplexů. V těch mohou ligandy (resp. jejich donorové atomy) obsadit sousední (cis) nebo protilehlé vrcholy (trans). U oktaedrických komplexů typu [Ma3b3] mohou navíc existovat dvě geometrické formy lišící se polohou trojice donorových atomů. Ty mohou obsadit buď vrcholy jedné stěny oktaedru (faciální uspořádání), nebo tři polohy na „obvodu“ oktaedru (meridionální uspořádání). Čtvercové komplexy se čtyřmi různými ligandy pak mohou existovat ve třech geometricky izomerních formách.
Optická izomerie vzniká u opticky aktivních látek. Optické izomery (tzv. enantiomery nebo antipody) můžeme očekávat u takových látek, v jejichž struktuře není žádný prvek symetrie kromě identity (nemají osu, rovinu ani střed symetrie). Takové látky, které nazýváme chirální nebo asymetrické, se mohou vyskytovat ve dvou formách, které se k sobě mají jako předmět a jeho obraz v zrcadle (nebo jako levá a pravá ruka). Takové dva izomery vypadají na první pohled zcela stejně, ovšem nelze je žádným otáčením a posunováním ztotožnit.
Významnou vlastností chirálních látek je jejich schopnost otáčet rovinu polarizovaného světla– jsou tzv. opticky aktivní. Enantiomery mají téměř všechny fyzikální a chemické vlastnosti stejné. Liší se pouze tím, že otáčejí rovinu polarizovaného světla (světlo, jehož vlny „kmitají“ jen v jednom směru) každý na jinou stranu. Podle toho se označují jako levotočivé (dříve označované l nebo −) a pravotočivé (d nebo +). Obě formy se také mírně liší v indexu lomu a schopností absorbovat záření. Směs obou enantiomerů v molárním poměru 1 : 1 neotáčí rovinu polarizovaného světla a nazývá se racemická směs (racemát). Absolutní konfiguraci lze určit jedině kompletní rentgenostrukturní analýzou.
Optické izomery existují u čtvercových, tetraedrických a oktaedrických komplexů. U čtvercových komplexů je optická izomerie vzácná a může nastat pouze v případě vhodně nesymetrických ligandů. U tetraedrických komplexů by bylo možné očekávat větší rozšíření optické izomerie, protože každý tetraedrický komplex se čtyřmi různými ligandy musí být opticky aktivní. Takovéto komplexy je však obtížné připravit a tak i v tomto případě byly připraveny opticky aktivní látky pouze s vhodnými bidentátními ligandy. Nejčastěji se ovšem optická aktivita projevuje u oktaedrických komplexů. V podstatě každý oktaedrický komplex typu [M(aa)3] nebo cis-[M(aa)2L2] (kde aa je bidentátní ligand) může existovat ve dvou zrcadlově převrácených formách.
Pokud je ligand v takovém komplexu sám o sobě opticky aktivní (např. 1,2-propandiamin), pak se počet možných optických izomerů samozřejmě zvyšuje. Izomerům se v takovém případě říká diastereoizomery. Ty už se mohou lišit i jinými vlastnostmi, např. rozpustností, stabilitou,…

Ionizační izomerie vzniká, jestliže izomery poskytují v roztoku různé ionty. Příkladem dvojice ionizačních izomerů jsou [Pt(NH3)4Cl2]Br2 a [Pt(NH3)4Br2]Cl2 nebo [Co(NH3)5(SO4)]Br a [Co(NH3)5Br]SO4.
Hydrátová izomerie vzniká při rozdílné přítomnosti vody vázané uvnitř a mimo koordinační sféru. Typickým příkladem je CrCl3.6H2O, který existuje ve třech formách: [Cr(H2O)6]Cl3 (fialový), [Cr(H2O)5Cl]Cl2·H2O (světle zelený) a [Cr(H2O)4Cl2]Cl·2H2O (temně zelený).
Vazebná izomerie vzniká, když se v komplexu váže ligand s větším počtem donorových atomů, které přitom nemůže použít současně (ambidentátní ligandy). Při tom může teoreticky nastat situace, že se váže v jinak stejných sloučeninách jiným donorovým atomem. Případy, kdy jsou takové izomery izolovatelné, jsou řídké a omezují se v podstatě na komplexy NO2− a SCN−. Příklady vazebných izomerů jsou dvojice [Co(en)2(NO2)2]+, [Co(en)2(ONO)2]+ a [Pd(PPh3)2(NCS)2], [Pd(PPh3)2(SCN)2]. Abychom odlišili způsob vazby ligandů, uvádí se koordinovaný donorový atom ve vzorci jako první. Odlišují je též od sebe odlišným názvem nebo vyznačením donorového atomu. NO2− nazývá se nitro, ONO− nitrito, NCS− thiokyanato-N a SCN− thiokyanato-S.
Koordinační izomerie vzniká ve sloučeninách složených z komplexního kationtu i aniontu, který se může měnit rozdělením ligandů mezi oběma ionty, např. [Co(en)3][Cr(CN)6] a [Cr(en)3][Co(CN)6] nebo [PtII(NH3)4][PtIVCl6] a [PtIV(NH3)4Cl2][PtIICl4]. Izomery se v tomto případě liší fyzikálně-chemickými vlastnostmi.
Polymerační izomerie není izomerií v pravém slova smyslu. Některé komplexy existují ve formách jednoduchých (monomerních) a také jako dimery nebo trimery. Takové látky mají stejný sumární vzorec, ale liší se molekulovou hmotností. Např. látka sumárního vzorce [Pt(NH3)2Cl2] existuje ve dvou monomerních formách (cis a trans), ale také jako dimer [Pt(NH3)4][PtCl4] a trimer [Pt(NH3)3Cl]2[PtCl4].
Barevnost komplexů
[editovat | editovat zdroj]Látka je obecně barevná, pokud je schopna své vnitřní energetické přechody, vyžadující jisté množství energie dodané v podobě kvanta viditelného světla, vyzářit v podobě viditelného světla. Energie světelného kvanta E je dána rovnicí :
- E = hν
kde h je Planckova konstanta a ν frekvence. Pokud je látka schopna absorbovat určitou oblast vlnových délek viditelného světla (určitou „barvu“), pak se na bílém světle jeví zbarvena tzv. doplňkovou (komplementární) barvou, v jejímž spektru absorbované vlnové délky chybí. Doplňková barva se určuje pomocí diagramu chromaticity (na obrázku), doplňková barva (námi viditelná) je naproti barvě absorbované. Barevné komplexní sloučeniny tedy musí absorbovat vlnové délky viditelného světla, tedy v rozsahu asi 380 – 770 nm. Energie tohoto záření ovšem nepostačuje na přechod elektronu do orbitalu s vyšším kvantovým číslem (např. 3d→ 4p), proto je nutné předpokládat méně energeticky náročné elektronové přechody. Ukázalo se (zjednodušeně řečeno), že takovými vhodnými přechody mohou být tzv. d-d přechody elektronů mezi různými energetickými hladinami rozštěpených d-orbitalů, které zavedla teorie krystalového pole. Existuje relativně jednoduchá souvislost mezi vlnovou délkou nebo energií absorbovaného záření a silou ligandového pole komplexů – tedy energetickým rozdílem mezi rozštěpenými d-orbitaly. Čím vyšší síla ligandového pole, tím vyšší energii vyžaduje přeskok elektronu a tím kratší vlnovou délku světla komplex absorbuje. Změna zbarvení komplexu vlivem různých ligandů je základem dříve zmíněné spektrochemické řady, kde jsou ligandy seřazeny v podstatě podle klesající vlnové délky světla absorbovaného příslušnými komplexy. Závěrem je třeba zmínit, že barva komplexu není dána pouze absorbováním záření při d-d přechodech elektronů centrálního atomu. Energii viditelného záření mohou odpovídat i přechody elektronů centrálního atomu do prázdných orbitalů ligandu nebo naopak (absorpční pásy přenosu náboje, tzv. CT-přechody „charge transfer).
Magnetické vlastnosti
[editovat | editovat zdroj]Měření efektivního magnetického momentu μ, může být využito k určení počtu nepárových elektronů n, které obsahují paramagnetické látky, a tím v souladu s představami teorie valenčních vazeb (VB) a teorie krystalového pole (CF), k určení typu vazby, oxidačního stavu a stereochemie komplexu. V nejjednodušším případě to znamená vycházet z tzv. čistě spinového vzorce :
Tabulka zobrazuje orbitalové příspěvky (OP) oktaedricky a tetraedricky uspořádaných iontů dx.
Vzorec určuje pouze spinový moment hybnosti („rotace“ elektronu kolem osy) k celkovému magnetickému momentu. Zjištěné hodnoty jsou vesměs o něco vyšší, obsahují i orbitální moment hybnosti (pohyb elektronu kolem jádra). Tyto „odchylky“ se daří vysvětlit pouze teorii CF, což je jedna z jejích vlastností oproti teorii VB.
Orbitální moment hybnosti vzniká, pokud jsou alespoň dva degenerované orbitaly téhož typu obsazeny rozdílným způsobem. Elektron je pak schopen se otáčet okolo určité osy vzájemnou přeměnou degenerovaných orbitalů, což jsou přesně tytéž okolnosti, které vedou k základnímu termu T, zatímco základní termy A a E přicházejí v úvahu pouze tehdy, je-li naopak orbitální příspěvek vyloučen. Jelikož je štěpení oktaedrických a tetraedrických termů CF opačné, vede u každého iontu dx jedna z těchto stereochemií k základnímu termu T a druhá k základnímu termu A nebo B. Pokud se dá orbitální příspěvek určit, dají se od sebe obě stereochemie odlišit. V praxi se využívá měření závislosti efektivního magnetického momentu na teplotě. Spin-orbitalní interakce, příčina jemné struktury absorpčních spekter, způsobuje, že velikost štěpení termů T je u prvků první přechodné řady řádově stejná jako tepelná energie. Tepelné rozdělení elektronové populace mezi těmito úrovněmi komponent termu T vede ke vzniku teplotně závislého magnetického momentu a tato závislost je nejlepším ukazatelem orbitálního příspěvku k magnetickému momentu látky.
Stabilita komplexních sloučenin
[editovat | editovat zdroj]Konstanta stability (komplexity)
[editovat | editovat zdroj]Stabilitou komplexních sloučenin se rozumí jejich odolnost vůči rozpadu na volný centrální atom a ligandy. Lze ji také chápat jako snadnost vzniku komplexu z centrálního atomu ligandu (platí zcela obecně, že stabilnější sloučeniny snadněji vznikají). Stabilita komplexních sloučenin se nejčastěji studuje a posuzuje v jejich vodných roztocích. V tomto případě ale při vzniku komplexu jde spíše o náhradu molekul vody komplexního aquaiontu za jiný ligand. Rozpad komplexu je naopak náhrada ligandu molekulou vody.
- [M(H2O)x]+xL↔[MLx]+xH2O
Tuto skutečnost je dobré mít na paměti i když se voda v běžném zápisu konstanty stability vypouští. Tato rovnice se v běžném zjednodušeném tvaru uvádí :
- M+xL↔MLx
Číselně lze celkovou stabilitu komplexu vyjádřit jako převrácenou hodnotu rovnovážné konstanty disociační reakce. Komplexy ve skutečnosti nedisociují najednou stejně jako najednou nevznikají. Mohou odštěpovat (nebo vázat) ligandy postupně po jednom a vzniklé „meziprodukty“ mohou být také stabilní. Pro jednotlivé stupně odštěpování ligandů lze samozřejmě také vyjádřit konstanty stability. Jako příklad výpočtu konstanty stability (viz obrázek) použijeme postupnou koordinaci chloridových aniontů na železitý kationt. Celková konstanta stability se poté spočítá jako součin jednotlivých dílčích (konsekutivních) konstant (hranaté závorky ve výrazu znamenají rovnovážné koncentrace).:
Pro jeden konkrétní komplex vždy platí, že konsekutivní konstanty stability postupně klesají s množstvím ligandů, tedy K1 > K2 >…> Kn Tento pokles je celkem snadno pochopitelný. Konsekutivní konstanty stability se týkají vždy odštěpení pouze jednoho ligandu z komplexu. Čím více ligandů bude vázáno na centrální atom (čím větší bude n), tím snadněji se jeden z nich může odštěpit. Vysvětlení lze podat i tak, že čím je více ligandů k odštěpení, tím roste pravděpodobnost, že se jeden z nich skutečně odštěpí a tím je tedy menší příslušná konsekutivní konstanta stability.
Faktory ovlivňující stabilitu komplexů
[editovat | editovat zdroj]Hodnoty konstant stability komplexů jsou ovlivňovány řadou faktorů, které lze zhruba shrnout do tří následujících skupin.
- Vliv centrálního atomu na stabilitu komplexu nelze postihnout jednoduchým způsobem. Pro silně elektropozitivní prvky z 1. až 3. skupiny (včetně lanthanoidů) platí poměrně přesně, že stabilita komplexu roste s rostoucím nábojem a s klesajícím poloměrem centrálního atomu. To je způsobeno převažujícím iontovým charakterem interakce centrálního atomu s ligandy u těchto prvků. Pro komplexy přechodných kovů už tak jednoduchá závislost na oxidačním čísle a poloměru atomu neexistuje, protože se u nich mnohem výrazněji projevuje kovalentnost koordinační vazby a navíc se zde uplatňuje stabilizace elektronové konfigurace ligandovým polem (Stabilizační energie ligandového pole) Pro téměř všechny vysokospinové komplexy kovů v oxidačním stavu +2 platí pořadí stability komplexů dané tzv. Irwingovou – Williamsovou řadou: Mn < Fe < Co < Ni < Cu > Zn Pořadí stability nízkospinových komplexů se od této řady významně liší. Např. stabilita kyanokomplexů M2+ sleduje řadu V < Cr > Mn < Fe > Co > Ni > Zn Jak je možné snadno ověřit, odpovídá tato řada velmi dobře stabilizačním energiím ligandového pole (nezapadá pouze Mn).
- Vliv ligandu nejvýrazněji ovlivňující stabilitu komplexu je jeho dentacita (vaznost). Ligandy se dvěma nebo více donorovými atomy, které mohou s centrálním atomem uzavřít cyklická uspořádání, vykazují tzv. chelátový efekt, tj. významné zvýšení stability komplexů ve srovnání s monodentátními ligandy. Mezi nejstálejší komplexy patří cheláty s pěti a šestičlennými kruhy, v nichž úhly nejlépe odpovídají vazebným úhlům. Přitom bylo prokázáno, že pětičetné kruhy jsou stálejší v případě jednoduchých vazeb v kruhu, šestičlenné jsou výhodnější v přítomnosti dvojných vazeb. Menší kruhy pak již obvykle nejsou příliš stabilní díky vysokému pnutí. Z hlediska ligandu je pro stabilitu komplexu velmi významná bazicita ligandu.
- Vliv kombinace centrálního atomu a ligandu vysvětluje skutečnosti, že některé centrální atomy preferují určitý typ ligandu pro tvorbu stabilních komplexů. Byla tak zavedena koncepce tvrdých a měkkých Lewisových kyselin (centrálních atomů) a Lewisových bází (ligandů). Za tvrdé kyseliny se považují kovy z prvních tří skupin periodické soustavy, z ostatních kovů především hliník. Jsou to kovy velmi elektropozitivní, s relativně malým iontovým poloměrem, u kterých existují tendence k tvorbě převážně iontových vazeb. Měkkými kyselinami jsou naopak především těžké d-prvky z druhé a třetí periody v nízkém oxidačním stavu, tedy prvky poměrně dost zaplněnými d-orbitaly, které budou jevit ochotu svůj relativní přebytek elektronů sdílet ve spíše kovalentní vazbě. Tvrdé báze jsou především ty ligandy, které mají relativně malé, ale silně elektronegativní donorové atomy (O, N, F). Z běžných ligandů jsou to amoniak, alifatické aminy, voda, hydroxidový anion, ethery, anionty kyslíkatých kyselin a fluoridy. Měkkými bázemi pak jsou především ligandy s těžšími donorovými atomy (S, P, As), π-donorové ligandy (acetylen, benzen), kyanidy, CO a těžší halogenidy.
Související články
[editovat | editovat zdroj]- Koordinační chemie
- Ligand
- Centrální atom
- Názvosloví koordinačních sloučenin
- Koordinační vazba
- Koordinační číslo
- Izomerie koordinačních sloučenin
- Barevnost komplexů
- Stabilita komplexních sloučenin
- Magnetické vlastnosti koordinačních sloučenin
Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu komplexní sloučenina na Wikimedia Commons
Obrázky, zvuky či videa k tématu komplexní sloučenina na Wikimedia Commons
Literatura
[editovat | editovat zdroj]- Dr. Heinrich Remy, Anorganická chemie 2. díl, 1. vydání 1961
- N. N. Greenwood – A. Earnshaw, Chemie prvků 2. díl, 1. vydání 1993 ISBN 80-85427-38-9
- Jursík F.: Anorganická chemie kovů. 1. vyd. 2002. ISBN 80-7080-504-8 (elektronická verze)

